canny 算子python实现

1. Canny介绍

Canny算子与Marr（LoG）边缘检测方法类似，也属于是先平滑后求导数的方法。John Canny研究了最优边缘检测方法所需的特性，给出了评价边缘检测性能优劣的三个指标：

• 1  好的信噪比，即将非边缘点判定为边缘点的概率要低，将边缘点判为非边缘点的概率要低；
• 2  高的定位性能，即检测出的边缘点要尽可能在实际边缘的中心；
• 3  对单一边缘仅有唯一响应，即单个边缘产生多个响应的概率要低，并且虚假响应边缘应该得到最大抑制。

2. Canny检测实现过程

第一步：灰度化 

第二步：高斯滤波 

首先生成二维高斯分布矩阵：

然后与灰度图像进行卷积实现滤波：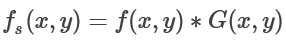

第三步：计算梯度值和方向 

求变化率时，对于一元函数，即求导；对于二元函数，求偏导。 数字图像处理中，用一阶有限差分近似求取灰度值的梯度值(变化率)。
             (即：使差商(Δf/Δx)近似取代微商(∂f/∂x)。求灰度的变化率，分别取x和y方向上相邻像素做差，代替求取x和y

方向一阶偏导) 。

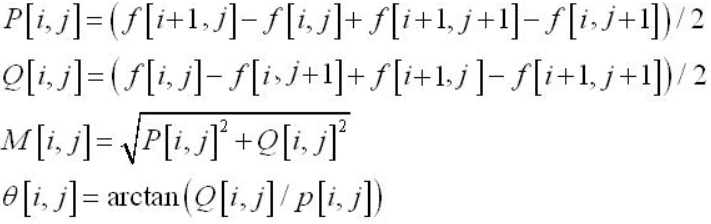
其中f为图像灰度值，P代表X方向梯度幅值，Q代表Y方向 梯度幅值，M是该点幅值，Θ是梯度方向，也就是角度。

注：图像梯度方向与边缘方向互相垂直：

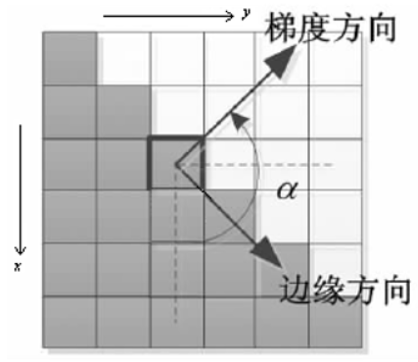
第四步：非极大值抑制（NMS）

             通俗意义上是指寻找像素点局部最大值。沿着梯度方向，比较它前面和后面的梯度值。在沿其方向上邻域的梯度幅值最大，则保留；否则，抑制。

具体参考此文：canny 非极大值抑制 NMS

可以进行插值来提高结果。

第五步：双阈值的选取、边缘连接

• 选取高阈值T H 和低阈值T L ，比率为2:1或3:1。（一般取TH =0.3 或 0.2, TL =0.1 ）
• 取出非极大值抑制后的图像中的最大梯度幅值，重新定义高低阈值。即：T H ×Max,T L ×Max  。(当然可以自己给定)
• 将小于TL 的点抛弃，赋0；将大于T H 的点立即标记（这些点就是边缘点），赋1。
• 将大于TL ，小于TH 的点使用8连通区域确定（即：只有与TH 像素连接时才会被接受，成为边缘点，赋1）  。

3. Canny检测Python实现

具体实现略有不同，例如：

高斯矩阵的实现过程、梯度幅值的实现过程、非极大值抑制的角度选取（可以选0，45，90，135）、边缘检测的实现过程。

# -*- coding: utf-8 -*-
"""
Created on Thu Dec  7 21:12:41 2017

@author: L.P.S
"""

import matplotlib.pyplot as plt
import numpy as np
import math

img = plt.imread('G:\\360downloads\\lps.png')

sigma1 = sigma2 = 1
sum = 0

gaussian = np.zeros([5, 5])
for i in range(5):
    for j in range(5):
        gaussian[i,j] = math.exp(-1/2 * (np.square(i-3)/np.square(sigma1)           #生成二维高斯分布矩阵
                        + (np.square(j-3)/np.square(sigma2)))) / (2*math.pi*sigma1*sigma2)
        sum = sum + gaussian[i, j]

gaussian = gaussian/sum
# print(gaussian)

def rgb2gray(rgb):
    return np.dot(rgb[...,:3], [0.299, 0.587, 0.114])

# step1.高斯滤波
gray = rgb2gray(img)
W, H = gray.shape
new_gray = np.zeros([W-5, H-5])
for i in range(W-5):
    for j in range(H-5):
        new_gray[i,j] = np.sum(gray[i:i+5,j:j+5]*gaussian)   # 与高斯矩阵卷积实现滤波 

# plt.imshow(new_gray, cmap="gray")

# step2.增强 通过求梯度幅值
W1, H1 = new_gray.shape
dx = np.zeros([W1-1, H1-1])
dy = np.zeros([W1-1, H1-1])
d = np.zeros([W1-1, H1-1])
for i in range(W1-1):
    for j in range(H1-1):
        dx[i,j] = new_gray[i, j+1] - new_gray[i, j]
        dy[i,j] = new_gray[i+1, j] - new_gray[i, j]
        d[i, j] = np.sqrt(np.square(dx[i,j]) + np.square(dy[i,j]))   # 图像梯度幅值作为图像强度值

# plt.imshow(d, cmap="gray")

# setp3.非极大值抑制 NMS
W2, H2 = d.shape
NMS = np.copy(d)
NMS[0,:] = NMS[W2-1,:] = NMS[:,0] = NMS[:, H2-1] = 0
for i in range(1, W2-1):
    for j in range(1, H2-1):

        if d[i, j] == 0:
            NMS[i, j] = 0
        else:
            gradX = dx[i, j]
            gradY = dy[i, j]
            gradTemp = d[i, j]

            # 如果Y方向幅度值较大
            if np.abs(gradY) > np.abs(gradX):
                weight = np.abs(gradX) / np.abs(gradY)
                grad2 = d[i-1, j]
                grad4 = d[i+1, j]
                # 如果x,y方向梯度符号相同
                if gradX * gradY > 0:
                    grad1 = d[i-1, j-1]
                    grad3 = d[i+1, j+1]
                # 如果x,y方向梯度符号相反
                else:
                    grad1 = d[i-1, j+1]
                    grad3 = d[i+1, j-1]

            # 如果X方向幅度值较大
            else:
                weight = np.abs(gradY) / np.abs(gradX)
                grad2 = d[i, j-1]
                grad4 = d[i, j+1]
                # 如果x,y方向梯度符号相同
                if gradX * gradY > 0:
                    grad1 = d[i+1, j-1]
                    grad3 = d[i-1, j+1]
                # 如果x,y方向梯度符号相反
                else:
                    grad1 = d[i-1, j-1]
                    grad3 = d[i+1, j+1]

            gradTemp1 = weight * grad1 + (1-weight) * grad2
            gradTemp2 = weight * grad3 + (1-weight) * grad4
            if gradTemp >= gradTemp1 and gradTemp >= gradTemp2:
                NMS[i, j] = gradTemp
            else:
                NMS[i, j] = 0

# plt.imshow(NMS, cmap = "gray")

# step4. 双阈值算法检测、连接边缘
W3, H3 = NMS.shape
DT = np.zeros([W3, H3])
# 定义高低阈值
TL = 0.2 * np.max(NMS)
TH = 0.3 * np.max(NMS)
for i in range(1, W3-1):
    for j in range(1, H3-1):
        if (NMS[i, j] < TL):
            DT[i, j] = 0
        elif (NMS[i, j] > TH):
            DT[i, j] = 1
        elif ((NMS[i-1, j-1:j+1] < TH).any() or (NMS[i+1, j-1:j+1]).any()
              or (NMS[i, [j-1, j+1]] < TH).any()):
            DT[i, j] = 1

plt.imshow(DT, cmap = "gray")            

4. 实验结果

                                     

原图                                                       双阈值：0.1*max， 0.3*max                                双阈值：0.2*max， 0.3*max

参考：

算法解剖系列-Canny边缘检测原理及实现

Canny边缘检测详解及编程实现

Canny算子中的非极大值抑制（Non-Maximum Suppression）分析

canny算子中非极大值抑制算法的理解

canny算子原理以及实现

图像学习之如何理解方向梯度直方图（Histogram Of Gradient）

论文：一种改进非极大值抑制的Canny边缘检测算法