java--二叉树解析及基本实现

一.二叉树的结构
　　在进行链表结构开发的过程之中,会发现所有的数据按照首尾相连的状态进行保存,那么 在进行数据查询时为了判断数据是否存在,这种情况下它所面对的时间复杂度就是"O(n)",如果说它现在的数据量比较小(<30)是不会对性能造成什么影响的,而一旦保存的数据量很大,这个时候时间复杂度就会严重损耗程序的运行性能,那么对于数据的存储结构就必须发生改变,应该尽可能的减少检索次数为出发点进行设计.对于现在的数据结构而言,最好的性能就是"O(logn)",现在想要实现它,就可以使用二叉树的结构来完成.
　　如果想要实现一颗树结构的定义,那么就需要去考虑数据的存储形式,在二叉树的实现中,基本原理如下:取第一个保存的数据为根节点,当比根节点小或相等的数据需要放在根的左子树,而大于节点的数据要放在该节点的右子树.同时,在每一个树节点中需要保存的东西有如下:父节点,数据,左子树,右子树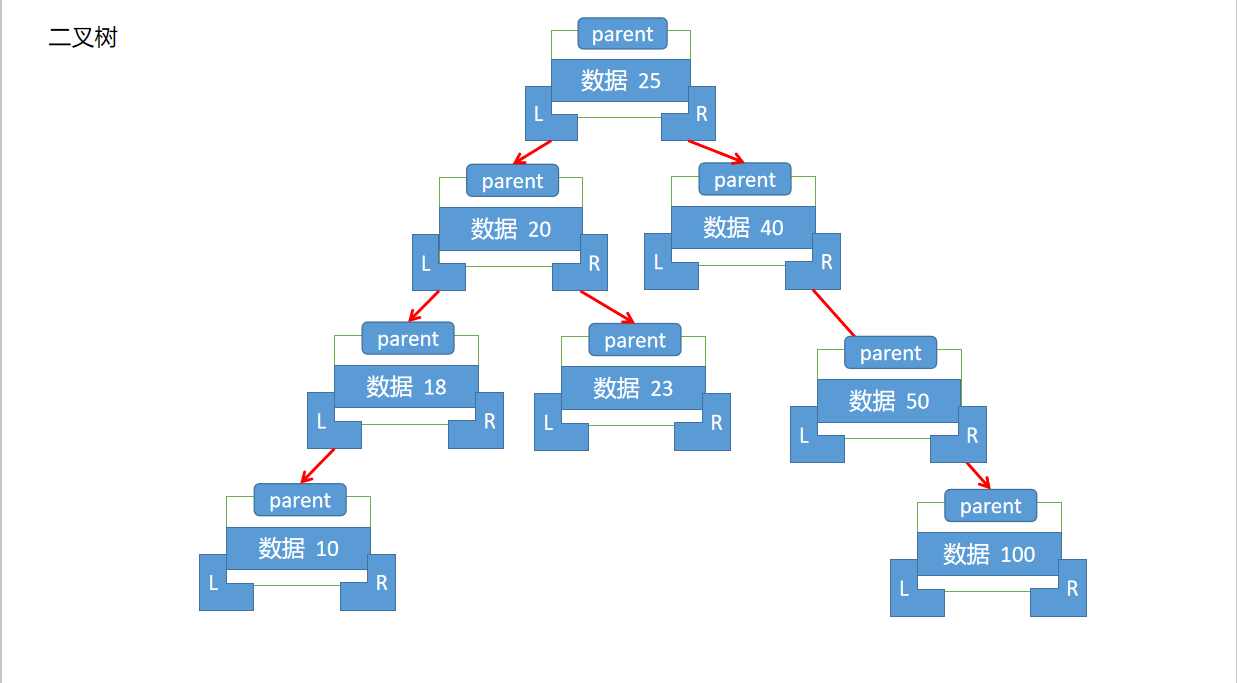

--当要进行数据检索时,此时就需要进行每个节点的判断,例如现在我们要查找数据23,那么我们可以知道23比25小,那么查询25的左子树,而25的左子树为20比数据23小,则查询他的右子树,其右子树23就是我们所需要的数据.其时间复杂度为O(logn).
--对于二叉树的查询,也有三种形式,分别为:前序遍历(根-左-右),中序遍历(左-根-右),后序遍历(左-右-根),以中序遍历为例,则以上的数据在中序遍历的时候最终的结果就是(10,18,20,23,25,40,50,100),可以发现二叉树中的内容全部都是排序的结果.

二.二叉树的基础实现
　　二叉树实现的关键问题在于数据的保存,而且数据由于牵扯到对象比较的问题,那么一定要有比较器的支持,而首选的比较器就是Comparable,以Person数据为例:

 package 常用类库.二叉树的实现;

 import javax.jws.Oneway;
 import java.lang.reflect.Array;
 import java.util.Arrays;

 /**
  * @author : S K Y
  * @version :0.0.1
  */
 class Person implements Comparable<Person> {
     private String name;
     private int age;

     public Person() {
     }

     public Person(String name, int age) {
         this.name = name;
         this.age = age;
     }

     public String getName() {
         return name;
     }

     public void setName(String name) {
         this.name = name;
     }

     public int getAge() {
         return age;
     }

     public void setAge(int age) {
         this.age = age;
     }

     @Override
     public int compareTo(Person o) {
         return this.age - o.age;
     }

     @Override
     public String toString() {
         return "Person{" +
                 "name='" + name + '\'' +
                 ", age=" + age +
                 '}';
     }
 }

 class BinaryTree<T extends Comparable<T>> {
     private class Node {
         private Comparable<T> data;     //存放Comparable,可以比较大小
         private Node parent;    //存放父节点
         private Node left;      //保存左子树
         private Node right;     //保存右子树

         public Node(Comparable<T> data) {        //构造方式直接实现数据的存储
             this.data = data;
         }

         /**
          * 实现节点数据的适当位置的存储
          *
          * @param newNode 创建的新节点
          */
         void addNode(Node newNode) {
             if (newNode.data.compareTo((T) this.data) <= 0) {   //比当前的节点小
                 if (this.left == null) {      //没有左子树,进行保存
                     this.left = newNode;
                     newNode.parent = this;      //保存父节点
                 } else {     //需要向左边继续判断
                     this.left.addNode(newNode);     //继续向下判断
                 }
             } else {     //比根节点的数据要大
                 if (this.right == null) {     //没有右子树
                     this.right = newNode;
                     newNode.parent = this;      //保存父节点
                 } else {
                     this.right.addNode(newNode);        //继续向下进行
                 }
             }
         }

         /**
          * 实现所有数据的获取处理,按照中序遍历的形式来完成
          */
         void toArrayNode() {
             if (this.left != null) {  //存在左子树
                 this.left.toArrayNode();        //递归调用
             }
             BinaryTree.this.returnData[BinaryTree.this.foot++] = this.data;
             if (this.right != null) {
                 this.right.toArrayNode();
             }
         }

     }

     /*===========以下是二叉树的功能实现=============*/
     private Node root;      //保存的根节点
     private int count;      //保存数据个数
     private Object[] returnData;        //返回的数据
     private int foot = 0;       //脚标控制

     /**
      * 进行数据的增加
      *
      * @param data 需要保存的数据
      * @throws NullPointerException 保存的数据不允许为空
      */
     public void add(Comparable<T> data) {
         if (data == null) {
             throw new NullPointerException("保存的数据不允许为空");
         }
         //所有的数据本身不具备有节点关系的匹配,那么一定要将其包装在Node类之中
         Node newNode = new Node(data);      //保存节点
         if (this.root == null) {      //表名此时没有根节点,那么第一个保存的数据将作为根节点
             this.root = newNode;
         } else {     //需要将其保存到一个合适的节点
             this.root.addNode(newNode);
         }
         count++;
     }

     /**
      * 以对象数组的形式返回数据,如果没有数据则返回null
      *
      * @return 全部数据
      */
     public Object[] toArray() {
         if (this.count == 0) return null;
         this.foot = 0;      //脚标清零
         this.returnData = new Object[count];
         this.root.toArrayNode();
         return returnData;
     }

 }

 public class MyBinaryTree {
     public static void main(String[] args) {
         BinaryTree<Person> tree = new BinaryTree<>();
         tree.add(new Person("小红", 20));
         tree.add(new Person("小光", 80));
         tree.add(new Person("小亮", 40));
         tree.add(new Person("小龙", 25));
         tree.add(new Person("小C", 77));
         tree.add(new Person("小D", 66));
         tree.add(new Person("小九", 35));
         tree.add(new Person("小Q", 54));
         Object[] objects = tree.toArray();
         System.out.println(Arrays.toString(objects));
     }
 }

--运行结果

[Person{name='小红', age=20}, Person{name='小龙', age=25}, Person{name='小九', age=35}, Person{name='小亮', age=40}, Person{name='小Q', age=54}, Person{name='小D', age=66}, Person{name='小C', age=77}, Person{name='小光', age=80}]

Process finished with exit code 0

--在以上的代码实现中采用了递归算法的操作,采用递归算法,相对而言其代码更加的简介明了,但是此时在进行数据添加的时候,只是实现了节点关系的保存,而这种关系保存后的结果就是所有的数据都是有序排列的.

三.数据删除
　　二叉树的数据删除操作是非常复杂的,因为在进行数据删除的时候需要考虑的情况是比较多的:
--1.如果删除的节点没有子节点,那么直接删除该节点即可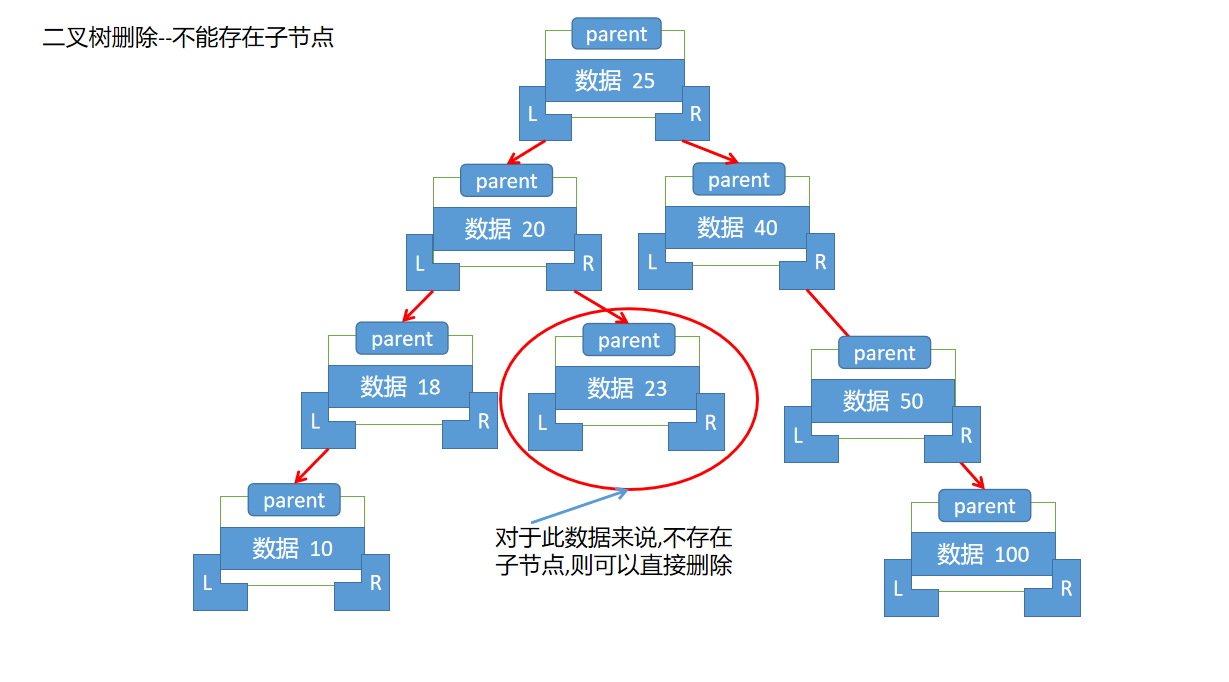

--2.如果待删除节点只有一个子节点,那么删除该节点之后,考虑两种情况的分析:
　　a.只有一个左子树:将其左子树放置于原来父节点的位置
　　b.只有一个右子树:也是将其右子树放置于原来父节点的位置
--3.如果删除节点存在两个子节点,那么删除该节点,首先需要找到当前节点的后继节点,这个后继节点就是其右子树的左侧叶子节点(及该节点下的最后一个左子树)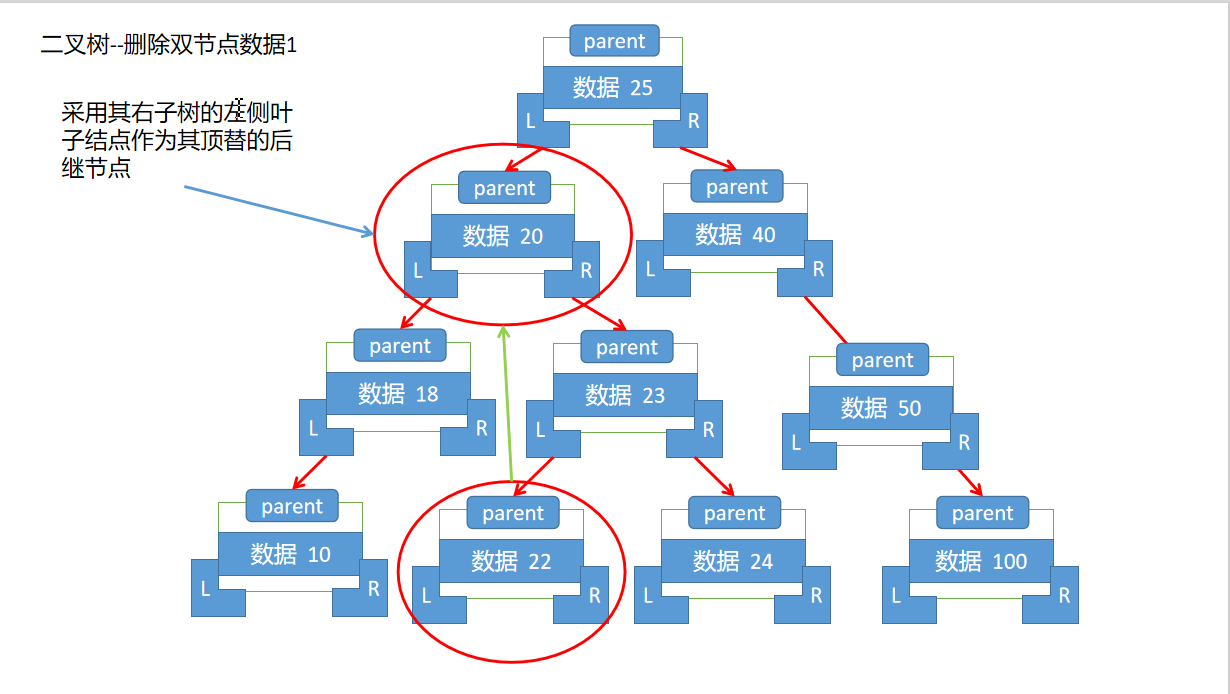

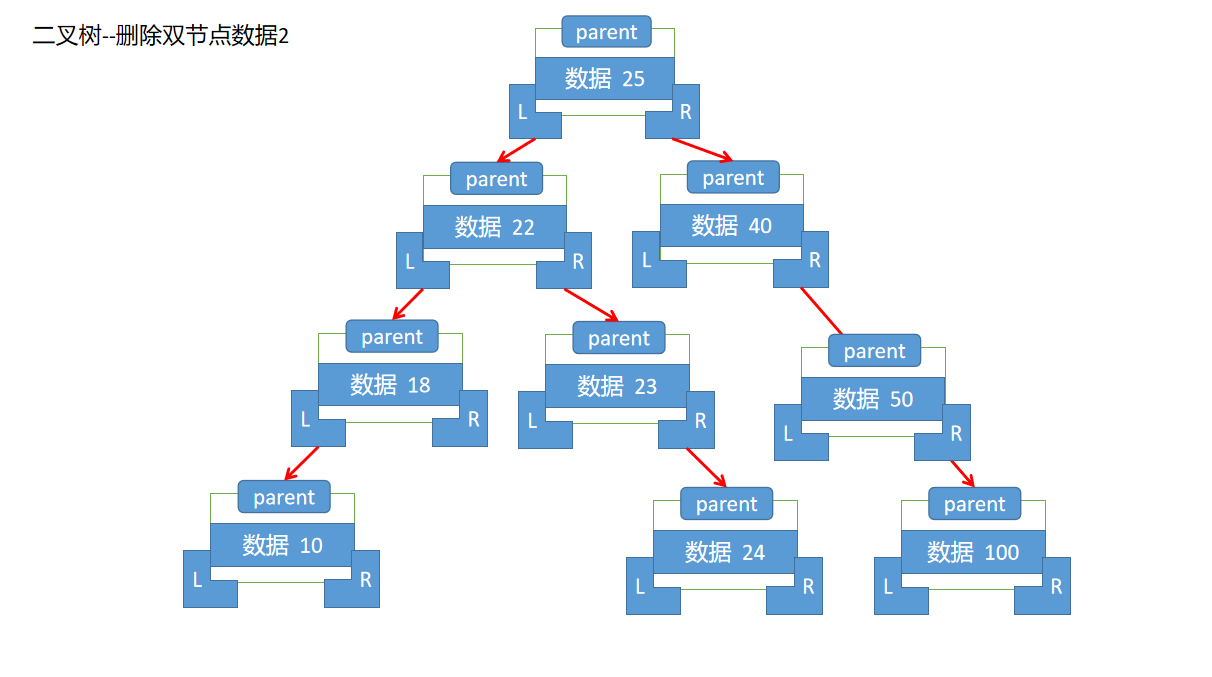
--具体的代码实现

 package 常用类库.二叉树的实现;

 import java.util.Arrays;

 /**
  * @author : S K Y
  * @version :0.0.1
  */
 class Person implements Comparable<Person> {
     private String name;
     private int age;

     public Person() {
     }

     public Person(String name, int age) {
         this.name = name;
         this.age = age;
     }

     public String getName() {
         return name;
     }

     public void setName(String name) {
         this.name = name;
     }

     public int getAge() {
         return age;
     }

     public void setAge(int age) {
         this.age = age;
     }

     @Override
     public int compareTo(Person o) {
         return this.age - o.age;
     }

     @Override
     public String toString() {
         return "Person{" +
                 "name='" + name + '\'' +
                 ", age=" + age +
                 '}';
     }
 }

 class BinaryTree<T extends Comparable<T>> {
     private class Node {
         private Comparable<T> data;     //存放Comparable,可以比较大小
         private Node parent;    //存放父节点
         private Node left;      //保存左子树
         private Node right;     //保存右子树

         public Node(Comparable<T> data) {        //构造方式直接实现数据的存储
             this.data = data;
         }

         /**
          * 实现节点数据的适当位置的存储
          *
          * @param newNode 创建的新节点
          */
         void addNode(Node newNode) {
             if (newNode.data.compareTo((T) this.data) <= 0) {   //比当前的节点小
                 if (this.left == null) {      //没有左子树,进行保存
                     this.left = newNode;
                     newNode.parent = this;      //保存父节点
                 } else {     //需要向左边继续判断
                     this.left.addNode(newNode);     //继续向下判断
                 }
             } else {     //比根节点的数据要大
                 if (this.right == null) {     //没有右子树
                     this.right = newNode;
                     newNode.parent = this;      //保存父节点
                 } else {
                     this.right.addNode(newNode);        //继续向下进行
                 }
             }
         }

         /**
          * 实现所有数据的获取处理,按照中序遍历的形式来完成
          */
         void toArrayNode() {
             if (this.left != null) {  //存在左子树
                 this.left.toArrayNode();        //递归调用
             }
             System.out.println(foot + " " + this.data + " parent:" + this.parent + " left:" + this.left + " right:" + this.right);
             BinaryTree.this.returnData[BinaryTree.this.foot++] = this.data;
             if (this.right != null) {
                 this.right.toArrayNode();
             }
         }

         @Override
         public String toString() {
             return "Node{" +
                     "data=" + data +
                     '}';
         }
     }

     /*===========以下是二叉树的功能实现=============*/
     private Node root;      //保存的根节点
     private int count;      //保存数据个数
     private Object[] returnData;        //返回的数据
     private int foot = 0;       //脚标控制

     /**
      * 进行数据的增加
      *
      * @param data 需要保存的数据
      * @throws NullPointerException 保存的数据不允许为空
      */
     public void add(Comparable<T> data) {
         if (data == null) {
             throw new NullPointerException("保存的数据不允许为空");
         }
         //所有的数据本身不具备有节点关系的匹配,那么一定要将其包装在Node类之中
         Node newNode = new Node(data);      //保存节点
         if (this.root == null) {      //表名此时没有根节点,那么第一个保存的数据将作为根节点
             this.root = newNode;
         } else {     //需要将其保存到一个合适的节点
             this.root.addNode(newNode);
         }
         count++;
     }

     /**
      * 返回树中当前的节点,如果存在
      *
      * @param data 所需要在树中获取节点的对象
      * @return 书中的当前节点, 如果不存在, 则返回null
      */
     private Node getNode(Comparable<T> data) {
         Node compareNode = BinaryTree.this.root; //当前比较的Node节点
         int i;      //当前的比较结果
         while ((i = data.compareTo((T) compareNode.data)) != 0) {
             if (i < 0) {    //当前节点比此节点小
                 compareNode = compareNode.left;
             } else {         //当前节点比此节点大
                 compareNode = compareNode.right;
             }
             if (compareNode == null) return null;         //不存在此节点,跳出循环,说明未找到数据
         }
         return compareNode;
     }

     /**
      * 判断当前节点是否存在
      *
      * @param data 需要判断的加节点
      * @return 如果当前节点存在则返回true, 不存在则返回false
      * @throws NullPointerException 查询的数据不允许为空
      */
     public boolean contains(Comparable<T> data) {
         if (data == null) return false;      //当前对象为空
         if (this.count == 0) return false;       //当前不存在数据
         return getNode(data) != null;
     }

     /**
      * 执行节点的删除处理
      *
      * @param data 需要删除的节点数据
      */
     public void remove(Comparable<T> data) {
         if (this.contains(data)) {       //要删除的数据存在
             //首先需要找到要删除的节点
             Node removeNode = this.getNode(data);
             if (removeNode.left == null && removeNode.right == null) {  //情况1:当前节点不存在子节点
                 //此时只要断开该删除节点的连接即可
                 if (removeNode.equals(removeNode.parent.left)) {
                     removeNode.parent.left = null;
                 } else {
                     removeNode.parent.right = null;
                 }
                 removeNode.parent = null;       //断开删除节点的引用
             } else if (removeNode.left == null) {       //此时说明只存在right子树
                 if (removeNode.equals(removeNode.parent.left)) {
                     removeNode.parent.left = removeNode.right;
                 } else {
                     removeNode.parent.right = removeNode.right;
                 }
                 removeNode.right.parent = removeNode.parent;
                 removeNode.parent = null;
             } else if (removeNode.right == null) {       //此时说明只存在left子树
                 if (removeNode.equals(removeNode.parent.left)) {
                     removeNode.parent.left = removeNode.left;
                 } else {
                     removeNode.parent.right = removeNode.left;
                 }
                 removeNode.left.parent = removeNode.parent;
                 removeNode.parent = null;
             } else {         //两边都有节点
                 Node needMoveNode = removeNode.right;       //所需移动的节点
                 System.out.println("needMoveNode: " + needMoveNode.data);
                 while (needMoveNode.left != null) {
                     needMoveNode = needMoveNode.left;
                 }       //此时已经获取删除节点的最小左节点,需要将其替代原来的节点
                 //考虑删除节点的右节点不存在左节点的情况,及删除节点的右节点就是最终的needMoveNode
                 if (needMoveNode.equals(needMoveNode.parent.right)) {
                     needMoveNode.parent.right = needMoveNode.right;
                 } else {
                     needMoveNode.parent.left = needMoveNode.right;
                 }
                 //替换节点的数据内容
                 removeNode.data = needMoveNode.data;
                 //断开needMoveNode的连接
                 needMoveNode.parent = null;

             }
             this.count--;
         }
     }

     /**
      * 以对象数组的形式返回数据,如果没有数据则返回null
      *
      * @return 全部数据
      */
     public Object[] toArray() {
         if (this.count == 0) return null;
         this.foot = 0;      //脚标清零
         System.out.println("count: " + count);
         this.returnData = new Object[count];
         this.root.toArrayNode();
         return returnData;
     }

 }

 public class MyBinaryTree {
     public static void main(String[] args) {
         //为了验证算法结构的准确性,将其内容设置为与图示相同
         BinaryTree<Person> tree = new BinaryTree<>();
         tree.add(new Person("小红", 25));
         tree.add(new Person("小光", 20));
         tree.add(new Person("小亮", 40));
         tree.add(new Person("小龙", 18));
         tree.add(new Person("小C", 23));
         tree.add(new Person("小D", 50));
         tree.add(new Person("小九", 10));
         tree.add(new Person("小Q", 22));
         tree.add(new Person("小Q", 24));
         tree.add(new Person("小Q", 100));
         Object[] objects = tree.toArray();
         System.out.println(Arrays.toString(objects));
         //删除23节点
         System.out.println("=======删除22节点========");
         tree.remove(new Person("小Q", 22));
         System.out.println(Arrays.toString(tree.toArray()));
         System.out.println("=======删除18节点========");
         tree.add(new Person("小Q", 22));
         tree.remove(new Person("小龙", 18));
         System.out.println(Arrays.toString(tree.toArray()));
         System.out.println("=======删除50节点========");
         tree.add(new Person("小龙", 18));
         tree.remove(new Person("小D", 50));
         System.out.println(Arrays.toString(tree.toArray()));
         System.out.println("=======删除23节点========");
         tree.add(new Person("小D", 50));
         tree.remove(new Person("小C", 23));
         System.out.println(Arrays.toString(tree.toArray()));
         System.out.println("=======删除20节点========");
         tree.add(new Person("小C", 23));
         tree.remove(new Person("小光", 20));
         System.out.println(Arrays.toString(tree.toArray()));
         System.out.println("=======删除25根节点========");
         tree.add(new Person("小光", 20));
         tree.remove(new Person("小红", 25));
         System.out.println(Arrays.toString(tree.toArray()));
     }
 }

--可以发现这种树结构的删除操作是非常繁琐的,所以如果不是必须的情况下不建议使用删除