Special Solutions:

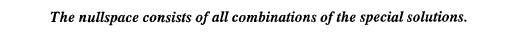
Notice what is special about s 1 and S2. They have ones and zeros in the last two components. Those components are "free" and we choose them specially. Then the first components -2 and -3 are determined by the equation Ax = 0. The first component is pivot, so it is not free. Special solutions come from our special choices.

A has rank=2, and the number of unknowns n=2, so the the number of free variables=n-r=0. Thus, no special solutions! What's more, A is invertible! B also doesn't have special solutions. But C has 2 special solutions.

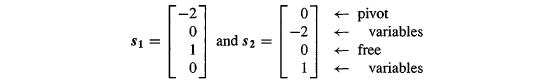
Rank:The numbers m and n give the size of a matrix-but not necessarily the true size of a linear system. An equation like 0 = 0 should not count, they can go up when elimination. The true size of A is given by its rank.

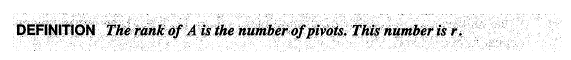
RREF(Reduced Row Echelon Form):

【读书笔记】：MIT线性代数(3):Special Solution, Rank and RREF的更多相关文章

  1. MySQL必知必会1-20章读书笔记

    MySQL备忘 目录 目录 使用MySQL 检索数据 排序检索数据 过滤数据 数据过滤 用通配符进行过滤 用正则表达式进行搜索 创建计算字段 使用数据处理函数 数值处理函数 汇总数据 分组数据 使用子 ...

  2. 《3D Math Primer for Graphics and Game Development》读书笔记1

    <3D Math Primer for Graphics and Game Development>读书笔记1 本文是<3D Math Primer for Graphics and ...

  3. 【英语魔法俱乐部——读书笔记】 3 高级句型-简化从句&倒装句(Reduced Clauses、Inverted Sentences) 【完结】

    [英语魔法俱乐部——读书笔记] 3 高级句型-简化从句&倒装句(Reduced Clauses.Inverted Sentences):(3.1)从属从句简化的通则.(3.2)形容词从句简化. ...

  4. 远程办公《Remote》读书笔记：中国程序员在家上班月入过六万不是梦

    这不是一本新书,这是一本很值得中国程序员看的老书,所以我不是来做卖新书广告的:) 但它的确是一本好书,这本书在Amazon上3个business categories排第一.作者Jason Fried ...

  5. 《Linux内核设计与实现》读书笔记（十一）- 定时器和时间管理【转】

    转自:http://www.cnblogs.com/wang_yb/archive/2013/05/10/3070373.html 系统中有很多与时间相关的程序(比如定期执行的任务,某一时间执行的任务 ...

  6. MIT线性代数课程 总结与理解-第一部分

    概述 个人认为线性代数从三个角度,或者说三个工具来阐述了线性关系,分别是: 向量 矩阵 空间 这三个工具有各自的一套方法,而彼此之间又存在这密切的联系,通过这些抽象出来的工具可以用来干一些实际的活,最 ...

  7. 《Python神经网络编程》的读书笔记

    文章提纲 全书总评 读书笔记 C01.神经网络如何工作? C02.使用Python进行DIY C03.开拓思维 附录A.微积分简介 附录B.树莓派 全书总评 书本印刷质量:4星.纸张是米黄色,可以保护 ...

  8. linux内核分析 1、2章读书笔记

    一.linux历史 20世纪60年代,MIT开发分时操作系统(Compatible TIme-Sharing System),支持30台终端访问主机: 1965年,Bell实验室.MIT.GE(通用电 ...

  9. 【读书笔记】《Computer Organization and Design: The Hardware/Software Interface》(1)

    笔记前言: <Computer Organization and Design: The Hardware/Software Interface>,中文译名,<计算机组成与设计:硬件 ...

随机推荐

  1. go 学习之fmt包

    基本模式fmt 方法可以大致分为 print, scan两类, 根据基础方法可以构建特定方法. Print 将参数写入字符串或io.writer scan 从字符串或 io.Reader 读取指定数据 ...

  2. VS code 生成html模板快捷键

    第一步:在空html文档中输入   ! 第二步:按下tab键.

  3. 卷积神经网络CNN原理以及TensorFlow实现

    在知乎上看到一段介绍卷积神经网络的文章,感觉讲的特别直观明了,我整理了一下.首先介绍原理部分. [透析] 卷积神经网络CNN究竟是怎样一步一步工作的? 通过一个图像分类问题介绍卷积神经网络是如何工作的 ...

  4. Zookeeper3.4.14集群搭建

    环境: 3台centos7.4 1. 下载release:wget https://mirrors.tuna.tsinghua.edu.cn/apache/zookeeper/zookeeper-3. ...

  5. 【LeetCode】线段树 segment-tree（共9题）+ 树状数组 binary-indexed-tree（共5题）

    第一部分---线段树:https://leetcode.com/tag/segment-tree/ [218]The Skyline Problem [307]Range Sum Query - Mu ...

  6. mongdb 副本集的原理、搭建、应用

    在了解了这篇文章之后,可以进行该篇文章的说明和测试.MongoDB 副本集(Replica Set)是有自动故障恢复功能的主从集群,有一个Primary节点和一个或多个Secondary节点组成.类似 ...

  7. jmeter 参数化2_CSV Data Set Config

    CSV Data Set Config:适用于参数取值范围较大的时候使用,该方法具有更大的灵活性 操作路径:HTTP取样器-->Add-->Config Element-->CSV ...

  8. Java对象流与序列化学习

    对象流与序列化 对象流有两个类 ObjectOutputStream:将java对象的基本数据类型和图形写入OutputStream ObjectInputStream:对以前使用ObjectOutp ...

  9. 设置Oracle PL/SQL时间显示格式NLS_TIMESTAMP_FORMAT

    Oracle中TIMESTAMP时间的显示格式   Oracle数据库的时间字段我们通常是使用timestamp 格式,在未做设置前, 查询出来的数据类似于“27-1月 -08 12.04.35.87 ...

  10. cocos2D-X 打包

    { //首先有java jdk,android sdk,android ndk //用android studio  import //匹配gradle 的版本 有些gradle可能下载不下来,不用慌 ...