python 递归，深度优先搜索与广度优先搜索算法模拟实现

一、递归原理小案例分析

（1）# 概述

递归：即一个函数调用了自身，即实现了递归 凡是循环能做到的事，递归一般都能做到！

（2）# 写递归的过程

1、写出临界条件

2、找出这一次和上一次关系

3、假设当前函数已经能用，调用自身计算上一次的结果，再求出本次的结果

（3）案例分析：求1+2+3+...+n的数和

# 概述
'''
递归：即一个函数调用了自身，即实现了递归
凡是循环能做到的事，递归一般都能做到！

'''

# 写递归的过程
'''
1、写出临界条件
2、找出这一次和上一次关系
3、假设当前函数已经能用，调用自身计算上一次的结果，再求出本次的结果
'''

# 问题：输入一个大于1 的数，求1+2+3+....
def sum(n):
    if n==1:
        return 1
    else:
        return n+sum(n-1)

n=input("请输入：")
print("输出的和是:",sum(int(n)))

'''
输出：
请输入：4
输出的和是: 10
'''

#__author:"吉*佳"
#date: 2018/10/21 0021
#function:

import os
def  getAllDir(path):
    fileList = os.listdir(path)
    print(fileList)
    for fileName in fileList:
        fileAbsPath = os.path.join(path,fileName)
        if os.path.isdir(fileAbsPath):
            print("$$目录$$：",fileName)
            getAllDir(fileAbsPath)
        else:
            print("**普通文件！**",fileName)
    # print(fileList)
    pass

getAllDir("G:\\")

输出结果如下：

二、深度遍历与广度遍历

（一）、深度优先搜索

说明：深度优先搜索借助栈结构来进行模拟

深度遍历示意图：

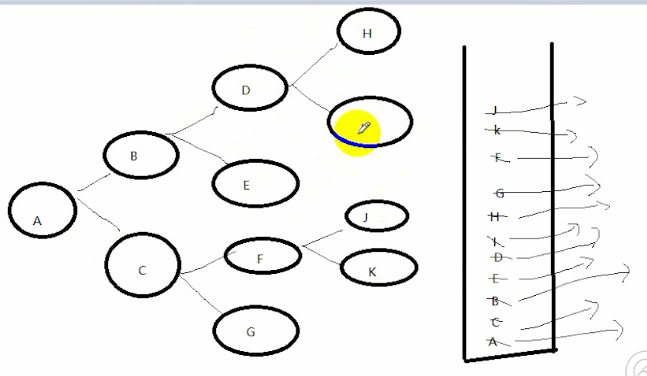
说明：

先把A压栈进去，在A出栈的同时把B C压栈进去，此时让B出栈的同时把DE压栈（C留着先不处理） 同理，在D出栈的时候，H I压栈，最后再从上往下

取出栈内还未出栈的元素，即达到深度优先遍历。

案例实践：利用栈来深度搜索打印出目录结构

程序代码：

#__author:"吉**"
#date: 2018/10/21 0021
#function:

# 深度优先遍历目录层级结构

import os

def getAllDirDP(path):
    stack = []
    # 压栈操作,相当于图中的A压入
    stack.append(path)

    # 处理栈，当栈为空的时候结束循环
    while len(stack) != 0:
        #从栈里取数据，相当于取出A，取出A的同时把BC压入
        dirPath = stack.pop()
        firstList = os.listdir(dirPath)
        #判断：是目录压栈，把该目录地址压栈，不是目录即是普通文件，打印
        for filename in firstList:
            fileAbsPath=os.path.join(dirPath,filename)
            if os.path.isdir(fileAbsPath):
                #是目录就压栈
                print("目录：",filename)
                stack.append(fileAbsPath)
            else:
                #是普通文件就打印即可，不压栈
                print("普通文件：",filename)

getAllDirDP(r'E:\[AAA]（千)全栈学习python\18-10-21\day7\temp\dir')

结果：

该过程示意图解释：（s-05-1部分）

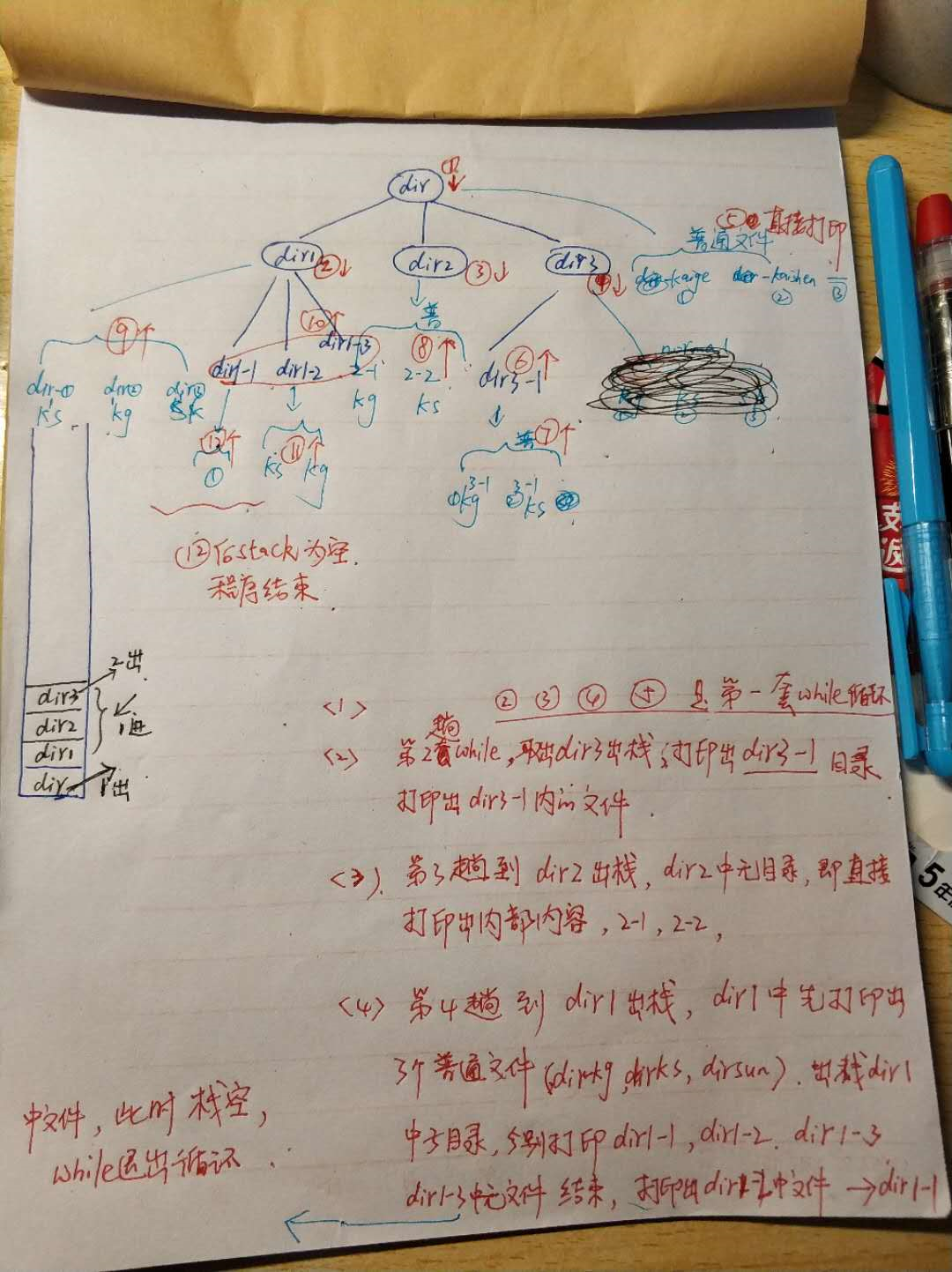
原理分析：

说明：

队列是 先进先出的模型。A先进队，在A出队的时候，C B入队，按图示，C出队，FG 入队，B出队，DE入队，

F出队，JK入队，G出队，无入队，D出队，H I入队，最后E J K H I出队，均无入队了，即每一层一层处理、

故：先进先出的队列结构实现了广度优先遍历。 先进后出的栈结构实现的是深度优先遍历。

代码实现：

其实深度优先和广度优先在代码书写上是差别不大的，基本相同，只是一个是使用栈结构（用列表进行模拟）

另一个（广度优先遍历）是使用了队列的数据结构来达到先进先出的目的。

#__author:"吉**"
#date: 2018/10/21 0021
#function:

# 广度优先搜索模拟
# 利用队列来模拟广度优先搜索

import os
import collections

def getAllDirIT(path):
    queue=collections.deque()
    #进队
    queue.append(path)

    #循环，当队列为空，停止循环
    while len(queue) != 0:
        #出队数据 这里相当于找到A元素的绝对路径
        dirPath = queue.popleft()
        # 找出跟目录下的所有的子目录信息，或者是跟目录下的文件信息
        dirList = os.listdir(dirPath)

        #遍历该文件夹下的其他信息
        for filename in dirList:
            #绝对路径
            dirAbsPath = os.path.join(dirPath,filename)

            # 判断：如果是目录dir入队操作，如果不是dir打印出即可
            if os.path.isdir(dirAbsPath):
                print("目录："+filename)
                queue.append(dirAbsPath)
            else:
                print("普通文件："+filename)

# 函数的调用
getAllDirIT(r'E:\[AAA]（千)全栈学习python\18-10-21\day7\temp\dir')

广度优先运行输出结构：

先图解：按照每一层从左到右遍历即可实现。

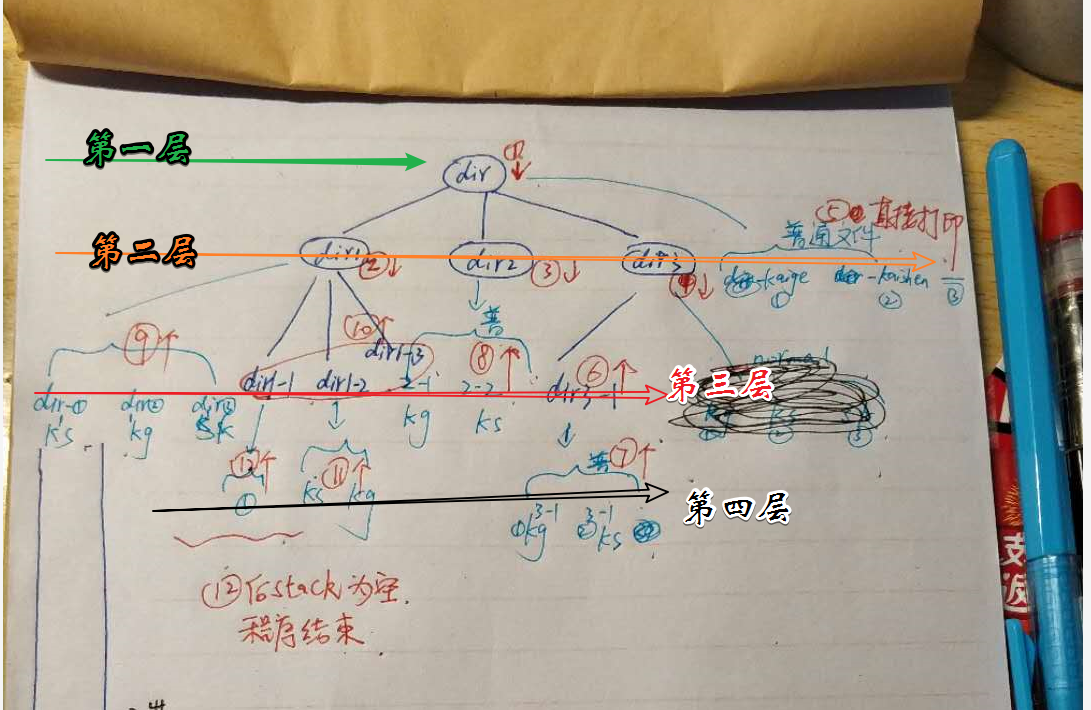
python 递归，深度优先搜索与广度优先搜索算法模拟实现