[LeetCode] 84. 柱状图中最大的矩形

题目链接 : https://leetcode-cn.com/problems/largest-rectangle-in-histogram/

题目描述:

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

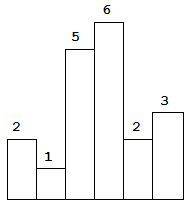
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

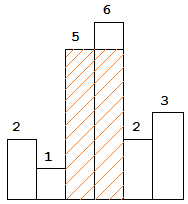
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

思路:

首先,想找到第i位置最大面积是什么?

是以i为中心,向左找第一个小于heights[i]的位置left_i;向右找第一个小于于heights[i]的位置right_i,即最大面积为heights[i] * (right_i - left_i -1),如下图所示:

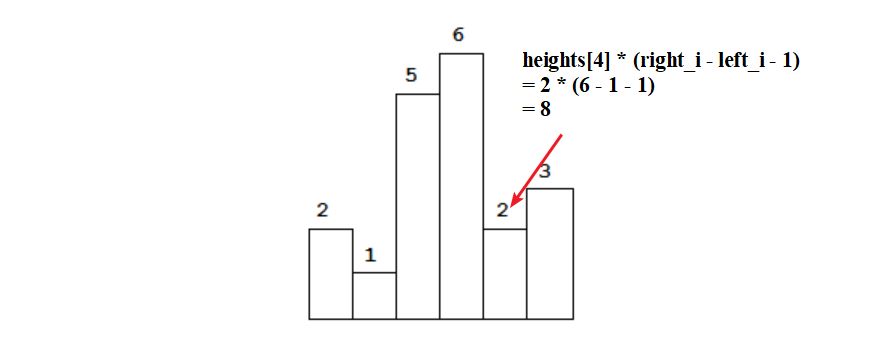
所以,我们的问题就变成如何找right_i 和left_i?

最简单的思路就是,就是暴力法,直接分别在i左右移动

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        res = 0
        n = len(heights)
        for i in range(n):
            left_i = i
            right_i = i
            while left_i >= 0 and heights[left_i] >= heights[i]:
                left_i -= 1
            while right_i < n and heights[right_i] >= heights[i]:
                right_i += 1
            res = max(res, (right_i - left_i - 1) * heights[i])
        return res

但是,这是一个时间复杂度为\(O(n^2)\),超时

接下来想办法优化.

思路一:

当我们找i左边第一个小于heights[i]如果heights[i-1] >= heights[i]其实就是和heights[i-1]左边第一个小于heights[i-1]一样.依次类推,右边同理.

思路二:栈

利用单调栈,我写过关于它一篇文章

维护一个单调递增的栈,就可以找到left_i 和right_i

代码:

思路一:

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        if not heights:
            return 0
        n = len(heights)
        left_i = [0] * n
        right_i = [0] * n
        left_i[0] = -1
        right_i[-1] = n
        for i in range(1, n):
            tmp = i - 1
            while tmp >= 0 and heights[tmp] >= heights[i]:
                tmp = left_i[tmp]
            left_i[i] = tmp
        for i in range(n - 2, -1, -1):
            tmp = i + 1
            while tmp < n and heights[tmp] >= heights[i]:
                tmp = right_i[tmp]
            right_i[i] = tmp
        # print(left_i)
        # print(right_i)
        res = 0
        for i in range(n):
            res = max(res, (right_i[i] - left_i[i] - 1) * heights[i])
        return res

java

class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) return 0;
        int n = heights.length;
        int[] left_i = new int[n];
        int[] right_i = new int[n];
        left_i[0] = -1;
        right_i[n - 1] = n;
        int res = 0;
        for (int i = 1; i < n; i++) {
            int tmp = i - 1;
            while (tmp >= 0 && heights[tmp] >= heights[i]) tmp = left_i[tmp];
            left_i[i] = tmp;
        }
        for (int i = n - 2; i >= 0; i--) {
            int tmp = i + 1;
            while (tmp < n && heights[tmp] >= heights[i]) tmp = right_i[tmp];
            right_i[i] = tmp;
        }
        for (int i = 0; i < n; i++) res = Math.max(res, (right_i[i] - left_i[i] - 1) * heights[i]);
        return res;
    }
}

思路二:

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        stack = []
        heights = [0] + heights + [0]
        res = 0
        for i in range(len(heights)):
            #print(stack)
            while stack and heights[stack[-1]] > heights[i]:
                tmp = stack.pop()
                res = max(res, (i - stack[-1] - 1) * heights[tmp])
            stack.append(i)
        return res

java

class Solution {
    public int largestRectangleArea(int[] heights) {
        int res = 0;
        Deque<Integer> stack = new ArrayDeque<>();
        int[] new_heights = new int[heights.length + 2];
        for (int i = 1; i < heights.length + 1; i++) new_heights[i] = heights[i - 1];
        //System.out.println(Arrays.toString(new_heights));
        for (int i = 0; i < new_heights.length; i++) {
            //System.out.println(stack.toString());
            while (!stack.isEmpty() && new_heights[stack.peek()] > new_heights[i]) {
                int cur = stack.pop();
                res = Math.max(res, (i - stack.peek() - 1) * new_heights[cur]);
            }
            stack.push(i);
        }
        return res;
    }
}