[CSP-S模拟测试]:d（贪心+树状数组）

题目传送门（内部题65）

---

输入格式

第一行，一个自然数$T$，代表数据组数。
对于每组数据：
第一行，一个正整数$n$，一个自然数$m$。
接下来$n$行，每行两个正整数，$a_i,b_i$。

---

输出格式

对于每组数据，输出一行，一个整数，代表答案。

---

样例

样例输入：

3
2 0
5 10
5 5
2 1
1 1
2 2
3 1
3 5
4 4
5 3

样例输出：

25
4
12

---

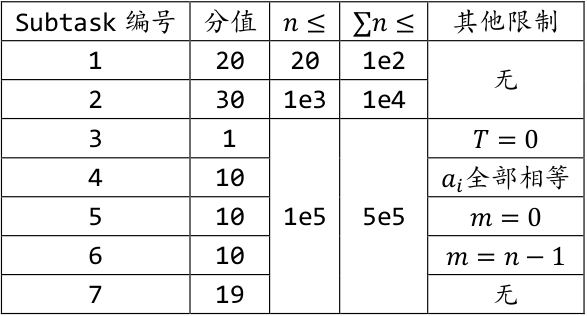
数据范围与提示

保证$0\leqslant m<n,a_i,b_i\leqslant 10^5$。

---

题解

题目并不难，考虑贪心，显然把$m$都用完一定不劣。

先将所有矩形按照$a_i$为第一维$b_i$为第二维排序，先将最后$m$个删去，将$b_i$加入树状数组，然后往前扫，不断改变策略，更新答案就好了。

时间复杂度：$\Theta(\sum n\log \sum n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int a,b;}e[100001];
int n,m;
int minb,maxb;
bool vis[100001];
int tr[100001];
long long ans;
bool cmp(rec a,rec b){return a.a==b.a?a.b<b.b:a.a<b.a;}
void pre_work()
{
	memset(tr,0,sizeof(tr));
	memset(vis,0,sizeof(vis));
	minb=0x3f3f3f3f;ans=maxb=0;
}
int lowbit(int x){return x&-x;}
void add(int x)
{
	for(int i=x;i<=maxb;i+=lowbit(i))
	tr[i]++;
}
int ask(int x)
{
	int res=0;
	for(int i=x;i;i-=lowbit(i))res+=tr[i];
	return res;
}
int main()
{
	int T;scanf("%d",&T);
	if(!T)return 0;
	while(T--)
	{
		pre_work();
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++)
		{
			scanf("%d%d",&e[i].a,&e[i].b);
			vis[e[i].b]=1;maxb=max(maxb,e[i].b);
		}
		sort(e+1,e+n+1,cmp);
		for(int i=n;i>m+1;i--)
		{
			add(e[i].b);
			minb=min(minb,e[i].b);
		}
		minb=min(minb,e[m+1].b);
		for(int i=m+1;i;i--)
		{
			add(e[i].b);
			if(e[i].a==e[i-1].a)continue;
			while(ask(minb)<m-i+2)minb++;
			while(!vis[minb])minb++;
			ans=max(ans,1LL*e[i].a*minb);
		}
		printf("%lld\n",ans);
	}
	return 0;
}

---

rp++