[CSP-S模拟测试]:最小值（DP+乱搞）

题目背景

　　$Maxtir$更喜欢序列的最小值。

---

题目传送门（内部题128）

---

输入格式

　　第一行输入一个正整数$n$和四个整数$A,B,C,D$。
　　第二行输入$n$个整数，第$i$个数表示$a_i$。

---

输出格式

　　输出一行一个整数$ans$表示答案。

---

样例

样例输入：

5 0 0 1 10
9 9 5 2 6

样例输出：

81

---

数据范围与提示

　　对于$10\%$的数据，满足$n\leqslant 100$
　　对于$20\%$的数据，满足$n\leqslant 1,000$
　　对于另外$20\%$的数据，满足$A=B=0,C\leqslant 0$
　　对于$100\%$的数据，满足$n\leqslant 2\times 10^5,\forall|f(a_i)|\leqslant 10^{13}$，输入数据均在整数$int$范围内

---

题解

第一眼，$\Theta(n^2)DP$，设$dp[i]$表示选到$i$的最大贡献。

转移很简单，枚举转移点即可。

第二眼，数据不好造，于是可以$j\geqslant \max(0,i-106)$就好啦……

其实我也不知道为什么$105$就$WA50$，$106$就直接$AC$了这也太巧了吧……

最后讲个故事，快搬好小板凳！！！

（话说你们为什么都爱听我讲故事额……

北岸大神：“动动，为什么我$QJ$还是会$TLE30$哇？！”

我：“？？？，不可能哇～“

北岸大神：”我调成$300$了！“

北岸大神：”我调成$100$了！“

北岸大神：”我$TM$都调成$1$了！！！“

我：”那你确定你写的是$j\geqslant \max(0,i-106)$嘛？“

北岸大神：”确定哇“

然而$\downarrow$

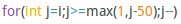
我：”……“

北岸大神：”窝槽“

左拐头朝下，小心别挂树叉上，忒疼。

时间复杂度：$\Theta(106\times n)$。

期望得分：$10$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,A,B,C,D;
long long a[200001];
long long dp[200001];
int main()
{
	memset(dp,-0x3f,sizeof(dp));
	scanf("%d%d%d%d%d",&n,&A,&B,&C,&D);
	for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
	dp[0]=0;
	for(int i=1;i<=n;i++)
	{
		int minn=max(0,i-106);
		long long res=a[i];
		for(int j=i-1;j>=minn;j--)
		{
			dp[i]=max(dp[i],dp[j]+A*res*res*res+B*res*res+C*res+D);
			res=min(res,a[j]);
		}
	}
	printf("%lld",dp[n]);
	return 0;
}

---

rp++