<背包>solution_CF366C_Dima and Salad

Dima and Salad

Dima, Inna and Seryozha have gathered in a room. That's right, someone's got to go. To cheer Seryozha up and inspire him to have a walk, Inna decided to cook something.

Dima and Seryozha have n fruits in the fridge. Each fruit has two parameters: the taste and the number of calories. Inna decided to make a fruit salad, so she wants to take some fruits from the fridge for it. Inna follows a certain principle as she chooses the fruits: the total taste to the total calories ratio of the chosen fruits must equal k. In other words, 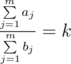, where aj is the taste of the j-th chosen fruit and bj is its calories.

Inna hasn't chosen the fruits yet, she is thinking: what is the maximum taste of the chosen fruits if she strictly follows her principle? Help Inna solve this culinary problem — now the happiness of a young couple is in your hands!

Inna loves Dima very much so she wants to make the salad from at least one fruit.

Input

The first line of the input contains two integers n, k (1 ≤ n ≤ 100, 1 ≤ k ≤ 10). The second line of the input contains n integers a1, a2, ..., an (1 ≤ ai ≤ 100) — the fruits' tastes. The third line of the input contains n integers b1, b2, ..., bn (1 ≤ bi ≤ 100) — the fruits' calories. Fruit number i has taste ai and calories bi.

Output

If there is no way Inna can choose the fruits for the salad, print in the single line number -1. Otherwise, print a single integer — the maximum possible sum of the taste values of the chosen fruits.

样例

input1

3 2
10 8 1
2 7 1

output1

18

input2

5 3
4 4 4 4 4
2 2 2 2 2

output2

-1

人话：

n个物品，k为倍数。每个物品有两个属性（ai和bi），求在满足所取物品的a属性和是b属性和的k倍的前提下，问a属性的最大值是多少

按照题意，就是要让我们选出一些组aibi，使的：

\(\frac{a_1+a_2+...+a_j}{b_1+b_2+...+b_j}=k\)，然后移项，得\(a_1+a_2+...+a_j=k(b_1+b_2+...+b_j)\)

得\((a_1-b_1k)+(a_2-b_2k)+...+(a_j-b_jk)=0\)，很像0/1分数规划，对不对

但是这题分类是背包

观察公式，发现这其实是一个容量为0的01背包，

我们可以把\(a_i-b_ik\)看作一个物品的体积，\(a_i\)看作价值，，然后一个标准的01背包模板

那么，背包的容量？容量为0怎么枚举呢？

先来想一想，\((a_i-b_ik)\)是不是有可能为负数？那么怎么办呢？

可以考虑开两个背包，容量分别为V和-V，那么加起来就抵消为0，正容量的背包处理正体积的，负容量的背包处理负体积的

很好，到这一步，套个模板就可以交啦！

Code:

#include <cstdio>
#include <cctype>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#define int long long
#define reg register
using namespace std;
const int MaxN=101;
const int MaxX=10000;
template <class t> inline void rd(t &s)
{
	s=0;
	reg char c=getchar();
	while(!isdigit(c))
		c=getchar();
	while(isdigit(c))
		s=(s<<3)+(s<<1)+(c^48),c=getchar();
	return;
}
int w[MaxN],c[MaxN];
int f[MaxX+1],g[MaxX+1];
int n,k;
inline void work()
{
	memset(f,0xc3,sizeof f);f[0]=0;
	memset(g,0xc3,sizeof g);g[0]=0;
	reg int W,C;
	for(int i=1;i<=n;++i)
		rd(w[i]);
	for(int i=1;i<=n;++i)
		rd(c[i]);
	for(int i=1;i<=n;++i)
	{
		W=w[i],C=c[i];
		w[i]=W-k*C;c[i]=W;
	}
	for(int i=1;i<=n;++i)
	{
//		printf("wi: %d   ci: %d\n",w[i],c[i]);
		if(w[i]>=0)
			for(int j=MaxX;j>=w[i];--j)
				f[j]=max(f[j],f[j-w[i]]+c[i]);
		else
			for(int j=MaxX;j>=-w[i];--j)
				g[j]=max(g[j],g[j+w[i]]+c[i]);
//		for(int j=1;j<=n;++j)
//			printf("fi: %d %d   ",f[i],g[i]);puts("");
	}
	reg int ans=-1;
	for(int i=0;i<=MaxX;++i)
		ans=max(ans,f[i]+g[i]);
	printf("%lld\n",!ans?-1:ans);
	return;
}
signed main(void)
{
	while(cin>>n>>k)
		work();
	return 0;
}