Cohen-Sutherland算法

Cohen-Sutherland算法

本算法又称为编码裁剪算法，算法的基本思想是对每 条直线段分三种情况处理：

（1）若点p1和p 2完全在裁剪窗口内

“简取”之

(2)若点p1(x1,y1)和p2(x2,y2)均在窗口外，且满足下 列四个条件之一：

对这四种类型的直线，“简弃”之

（3）如果直线段既不满足“简取”的条件，也不满足 “简弃”的条件？

需要对直线段按交点进 行分段，分段后判断直 线是“简取”还是“简 弃”。

每条线段的端点都赋以四 位二进制码D3D2D1D0，编 码规则如下：

窗口及其延长线所构 成了9个区域。根据该 编码规则：

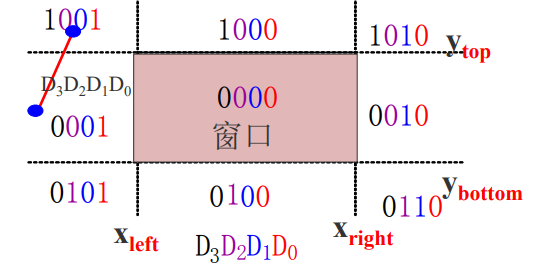
裁剪一条线段时，先 求出端点p1和p 2的编 码code1和code 2

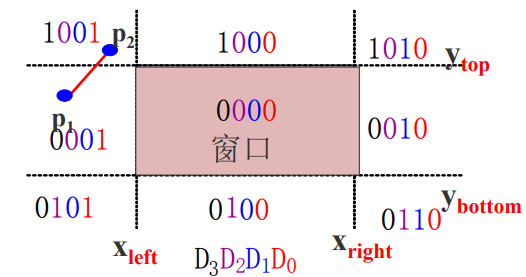
然后进行二进制“ 或 ” 运算和“ 与”运算

（1）若code1|code2=0 ，对直线段应简取之

（2）若code1&code2≠0，对直线段可简弃之

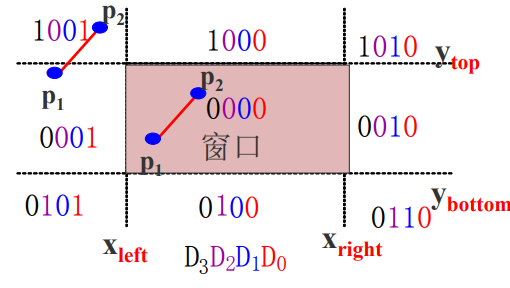
若上述两条件均不成立

则需求出直线段与窗口边界的交点在交 点处把线段一分为二

小结

Cohen-Sutherland算法用编码的方法实现了对直线段的裁剪

编码的思想在图形学中甚至在计算机科学里也是非常重要的 ，一个很简单的思想可以带来很了不起的作用。

比较适合两种情况：一是大部分线段完全可见；二是大部分 线段完全不可见。