MIT线性代数:15.子空间的投影
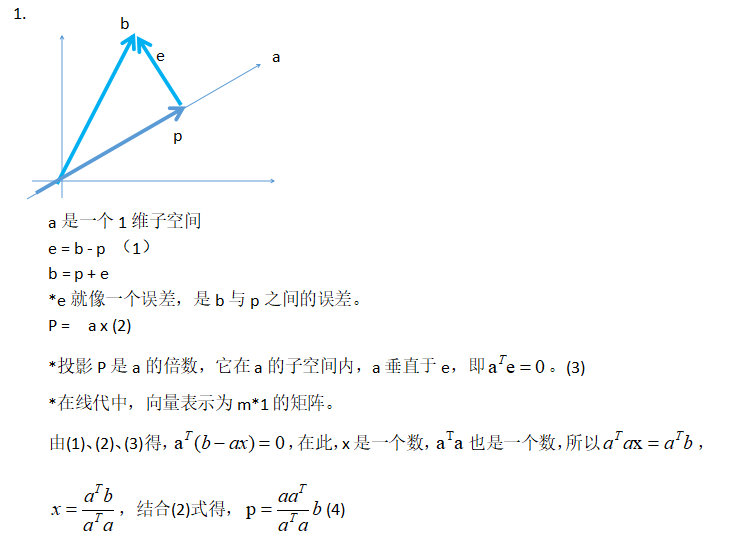


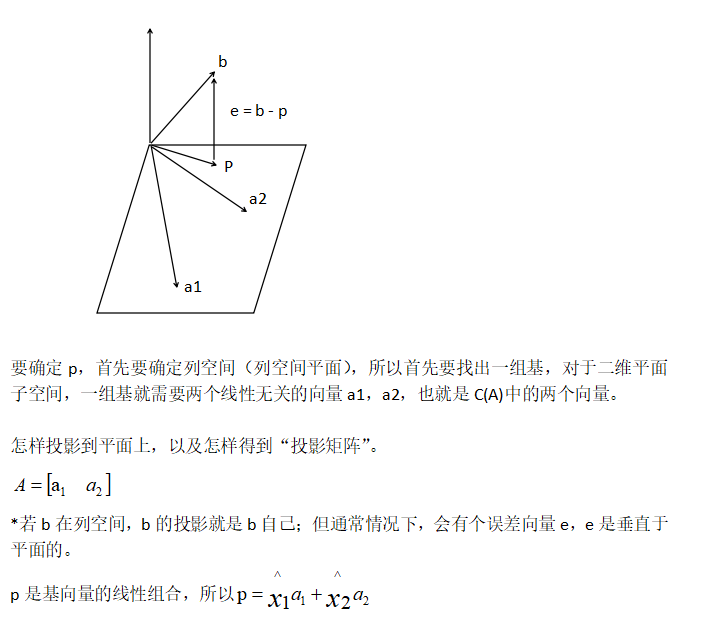


MIT线性代数:15.子空间的投影的更多相关文章
- MIT线性代数:16.投影矩阵和最小二乘
- MIT线性代数:10.4个基本子空间
- MIT线性代数课程 总结与理解-第一部分
概述 个人认为线性代数从三个角度,或者说三个工具来阐述了线性关系,分别是: 向量 矩阵 空间 这三个工具有各自的一套方法,而彼此之间又存在这密切的联系,通过这些抽象出来的工具可以用来干一些实际的活,最 ...
- MIT线性代数:22.对角化和A的幂
- MIT线性代数:21.特征值和特征向量
- MIT线性代数:20.克拉默法则,逆矩阵和体积
- MIT线性代数:19.行列式和代数余子式
- MIT线性代数:18.行列式及其特性
- MIT线性代数:17.正交矩阵和Cram-Schmidt正交化
随机推荐
- 瀑布流实例及懒加载(echo.js)
瀑布流布局: 图片等宽,不定高,按最低高度来顺序排列:实现方法:获取每次获取四行中最低高度对应的一行,将下一张加载的图片放在该位置,每次加载前都获取最低高度: ①请求图片的接口 地址此php文件 ...
- mac安装flask
1.1使用虚拟环境 输入以下命令可以检查系统是否安装了 virtualenv: $ virtualenv --version 大多数 Linux 发行版都提供了 virtualenv 包.例如,Ubu ...
- postman常用断言
1.Code is 200 断言状态码是200 2.contains string 断言respoonse body中包含string 3.json value check (检查JSON值)
- 【前端词典】几个有益的 CSS 小知识
今天偷个懒,不长篇大论,分享几个你可能不知道的 CSS 小知识. 样式的顺序 CSS 代码: HTML 代码: 记得之前这是一道比较火的 CSS 考题,当时好像是有不少的人答错(30% 以上) ...
- windows 7 专业版 64位 无法安装.Net 4.7版本解决方案
什么暂停windows update,改文件夹,再恢复windows update等等方法都试了,不行之后就觉得这才是终极解决方案. 不管你是win 7什么版本,你只需要下载安装对应系统的Window ...
- Spring Boot2 系列教程(十四)CORS 解决跨域问题
今天和小伙伴们来聊一聊通过CORS解决跨域问题. 同源策略 很多人对跨域有一种误解,以为这是前端的事,和后端没关系,其实不是这样的,说到跨域,就不得不说说浏览器的同源策略. 同源策略是由 Netsca ...
- [NOIp2011] luogu P1313 计算系数
继续水博客,待会回去上术学. 题目描述 给定一个多项式 (by+ax)k(by+ax)^k(by+ax)k ,请求出多项式展开后 xn×ymx^n \times y^mxn×ym 项的系数. Solu ...
- UVA10228 A Star not a Tree?
[返回模拟退火略解] 题目描述 一平面上有 nnn 个点 {Ai}\{A_i\}{Ai},求一个点 XXX 使得σ=∑i=1ndis(Ai,X)\sigma=\sum_{i=1}^{n}{dis(A ...
- MacOS访达增强工具-TotalFinder
TotalFinder 是Mac上最好用的Finder增强工具,TotalFinder 提供了多标签式浏览.拷贝路径.剪切文件.显示隐藏文件.双栏窗口模式.彩色标签等功能 彩色的标签 将彩色带回El ...
- POJ 3080 Blue Jeans(串)
题目网址:http://poj.org/problem?id=3080 思路: 以第一个DNA序列s为参考序列,开始做以下的操作. 1.将一个字母s[i]作为匹配串.(i为当前遍历到的下标) 2.遍历 ...
