Leetcode之深度优先搜索（DFS）专题-559. N叉树的最大深度（Maximum Depth of N-ary Tree）

Leetcode之深度优先搜索（DFS）专题-559. N叉树的最大深度（Maximum Depth of N-ary Tree）

深度优先搜索的解题详细介绍，点击

---

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

例如，给定一个 3叉树 :

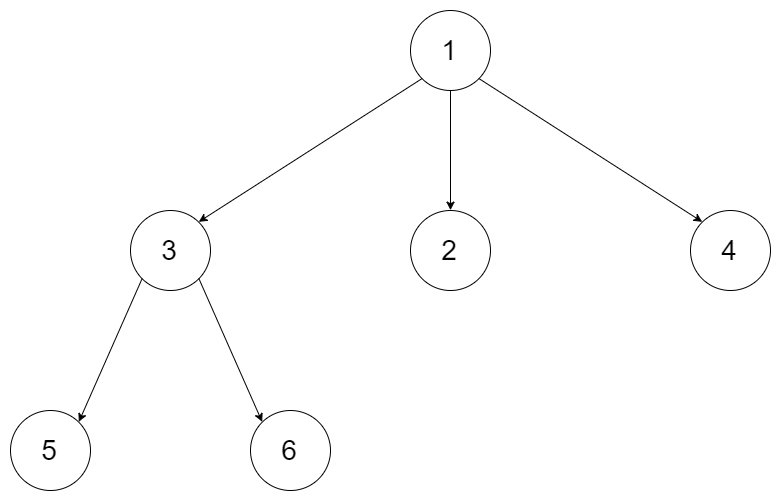
我们应返回其最大深度，3。

说明:

1. 树的深度不会超过 1000。
2. 树的节点总不会超过 5000。

　　　　　　

---

N叉树的遍历，和二叉树的遍历一样。

AC代码：

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val,List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
    public int maxDepth(Node root) {
        if(root==null) return 0;
        return dfs(root);
    }
    public int dfs(Node node){
        if(node==null) return 1;

        int maxx = 0;
        for(Node n:node.children){
            maxx = Math.max(maxx,dfs(n));
        }
        return maxx+1;

    }
}