NOIP2003神经网络[BFS]

题目背景

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

题目描述

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

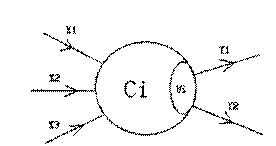
神经元〔编号为1）

图中，X1―X3是信息输入渠道，Y1－Y2是信息输出渠道，C1表示神经元目前的状态，Ui是阈值，可视为神经元的一个内在参数。

神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经无分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

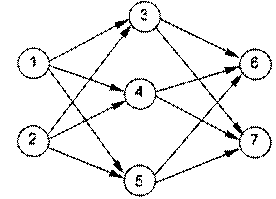
兰兰规定，Ci服从公式：（其中n是网络中所有神经元的数目）

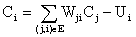
公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。

如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。

输入输出格式

输入格式：

输入文件第一行是两个整数n（1≤n≤100）和p。接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。再下面P行，每行由两个整数i，j及一个整数Wij，表示连接神经元i、j的边权值为Wij。

输出格式：

输出文件包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状态，两个整数间以空格分隔。仅输出最后状态大于零的输出层神经元状态，并且按照编号由小到大顺序输出！

若输出层的神经元最后状态均为 0，则输出 NULL。

输入输出样例

输入样例#1：

输出样例#1：

不就是个裸的bfs，按层递推就行了
没必要拓扑排序，初状态>0的一定是输入层，没有出边的一定是输出层

#include <iostream>

#include <cstdio>

#include <algorithm>

#include <cstring>

#include <cmath>

using namespace std;

const int N=,INF=1e9;

int n,m,u[N],c[N],a,b,w;

struct edge{

    int v,w,ne;

}e[N*N];

int h[N],cnt=;

inline void ins(int u,int v,int w){

    cnt++;

    e[cnt].v=v;e[cnt].w=w;e[cnt].ne=h[u];h[u]=cnt;

}

int q[N],head=,tail=,inq[N];

void bfs(){

    while(head<=tail){

        int now=q[head++];inq[now]=;//printf("bfs %d %d\n",now,c[now]);

        if(c[now]<=) continue;

        for(int i=h[now];i;i=e[i].ne){

            int v=e[i].v,w=e[i].w;

            c[v]+=w*c[now];

            if(!inq[v]) q[++tail]=v,inq[v]=,c[v]-=u[v];

        }

    }

}

int main(){

    scanf("%d%d",&n,&m);

    for(int i=;i<=n;i++) {

        scanf("%d%d",&c[i],&u[i]);

        if(c[i]!=) {q[++tail]=i;inq[i]=;}

    }

    for(int i=;i<=m;i++) scanf("%d%d%d",&a,&b,&w),ins(a,b,w);

    bfs();

    int flag=;

    for(int i=;i<=n;i++)

        if(h[i]==)

            if(c[i]>) flag=,printf("%d %d\n",i,c[i]);

    if(flag==) printf("NULL");

}