POJ 1228 Grandpa's Estate --深入理解凸包

题意： 判断凸包是否稳定。

解法： 稳定凸包每条边上至少有三个点。

这题就在于求凸包的细节了，求凸包有两种算法：

1.基于水平序的Andrew算法

2.基于极角序的Graham算法

两种算法都有一个类似下面的语句：

for(int i=0;i<n;i++) {
        while(m > 1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
        ch[m++] = p[i];
    }

这样的话，求出来就是最简凸包，即点数尽量少的凸包，因为Cross == 0的情况也被出栈了，所以一条凸包边上就会三点共线了。

我们把语句改下，把Cross.. <=0  改成 Cross.. < 0 ，那么求的就是最繁凸包，即可能一条凸包边上包含很多点也属于凸包的点。

即下面的情况：

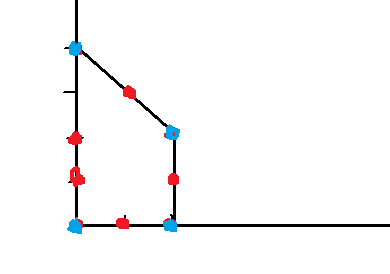
最简凸包即为蓝色的四个点。 最繁凸包求出的是所有蓝点和红点。

作为这个题，我们怎么求其实都可以：

1.如果求最简凸包，我们只需判断总共有多少个点在该凸包边上即可（端点也算），如果 < 3 ，则不符。

2.如果求的是最繁的凸包，就不能用上面的判法，因为怎么判都只有两个点了，这时候可以采用下面的方法：

假设要判断的边i，那么判断边i和边i-，边i和边i+1的夹角是否都为0（）。                                        ----XDruid

代码： （这里我用的是Andrew算法）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#define eps 1e-8
using namespace std;

struct Point{
    double x,y;
    Point(double x=, double y=):x(x),y(y) {}
    void input() { scanf("%lf%lf",&x,&y); }
};
typedef Point Vector;
int dcmp(double x) {
    if(x < -eps) return -;
    if(x > eps) return ;
    return ;
}
template <class T> T sqr(T x) { return x * x;}
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }
bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); }
bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; }
bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; }
bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) ==  && dcmp(a.y-b.y) == ; }
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }
double angle(Vector v) { return atan2(v.y, v.x); }

bool OnSegment(Point P, Point A, Point B) {         //端点不算
    return dcmp(Cross(A-P,B-P)) ==  && dcmp(Dot(A-P,B-P)) <= ;
}
int ConvexHull(Point* p, int n, Point* ch) {
    sort(p,p+n);
    int m = ;
    for(int i=;i<n;i++) {
        while(m >  && Cross(ch[m-]-ch[m-], p[i]-ch[m-]) <= ) m--;
        ch[m++] = p[i];
    }
    int k = m;
    for(int i=n-;i>=;i--) {
        while(m > k && Cross(ch[m-]-ch[m-], p[i]-ch[m-]) <= ) m--;
        ch[m++] = p[i];
    }
    if(n > ) m--;
    return m;
}
Point ch[],p[];

int main()
{
    int t,n,i,j;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(i=;i<n;i++) p[i].input();
        if(n <= ) { puts("NO"); continue; }
        int m = ConvexHull(p,n,ch);
        if(m <= ) { puts("NO"); continue; }
        for(i=;i<m;i++) {
            int cnt = ;
            for(j=;j<n;j++)
                if(OnSegment(p[j],ch[i],ch[(i+)%m]))
                    cnt++;
            if(cnt < ) break;
        }
        if(i == m) puts("YES");
        else       puts("NO");
    }
    return ;
}

现在终于对自己的凸包版有了全面的了解了，妈妈再也不用担心我用错凸包了。哈哈。