SciTech-Physics-Particle-Quantum Theories-Heisenberg Uncertainty Principle: 量子理论核心: 海森堡不确定性原理 的 数学公式 + 波函数 度量 量子粒子的空间位置分布

名词解释

• 动量: 一个vector, 既有 "速度"，也有"方向"。
• 波粒双性: 量子粒子(如电子)，既有粒子性，也有波动性。
• 波函数: 在量子力学，粒子的位置和动量都可以用波函数（(,)ψ(x,t)）来表示。
  
  波函数的平方给出粒子在某一位置出现的概率密度，但这个概率密度是扩展的，
  
  因而无法精确给出位置和动量的确切数值。
  
  量子力学上的波函数，可表示为“量子粒子在观测之前是处于一种叠加状态”。

Heisenberg Uncertainty Principle

数学表达 位置与动量 能量与时间	数学解析	波函数 描述量子位置的 不确定性(同心圆)	融合 数学公式+波函数

“海森堡不确定性原理”是量子力学的“一个核心概念”和“一项基本特征”，

它揭示微观世界的 某些物理量****不能同时精确地测量得到。

这一原理表达"量子粒子的行为"存在"原生不确定性"。

即“无法同时精确地”知道“粒子的'位置'和'动量'”。

这并不是由于测量技术的限制，而是由于自然界的根本特性。

这个原理由德国物理学家“维尔纳·海森堡”于1927年提出，成为量子力学的一项基本特征**。

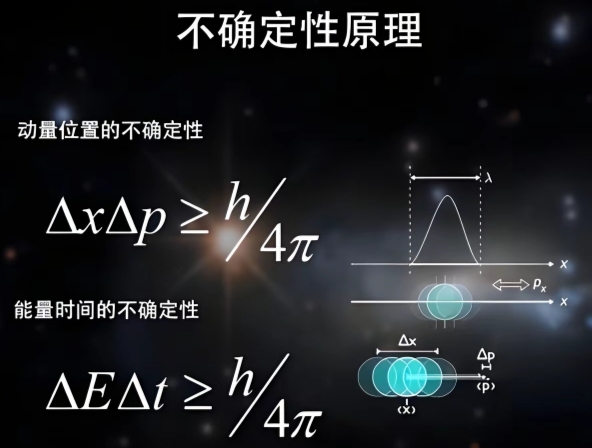
数学表达(海森堡不确定性原理)

海森堡不确定性原理 可以通过一个简单的数学公式来描述，

它关系到粒子的位置（）和动量（）的不确定性：

Δ⋅Δ ≥ℏ2Δx⋅Δp≥2ℏ

其中：

Δ 是 "粒子位置" 的 "不确定性"，即测量"粒子位置时"的"误差(或模糊度)"。

Δ 是 "粒子动量" 的 "不确定性"，即测量"粒子动量时"的"误差(或模糊度)"。

ℏ 是约化普朗克常数，它的数值为 \(1.054571 \times 10^{-34} \, \text{J·s}\)。

• 公式的含义：
  
  粒子的位置和动量的测量误差（不确定性）的乘积永远大于或等于一个常数 ℏ22ℏ。
  
  这表示: 如果你希望尽可能精确地测量一个粒子的位置，那么它的动量的测量误差就必须变大，反之亦然。

• 物理意义
  
  不可同时精确测量的位置和动量：
  
  这个原理揭示量子力学最根本的特性之一：粒子的位置和动量是无法同时精确测量的。
  
  越是精确测量位置，动量的不确定性就越大，反之亦然。
  
  这并不是由于测量技术的限制，而是由于自然界的根本特性。
  
  量子粒子无法被完全“确定”，它们的状态本身就存在一种“模糊性”。

  • 波动性和粒子性之间的关系：
    
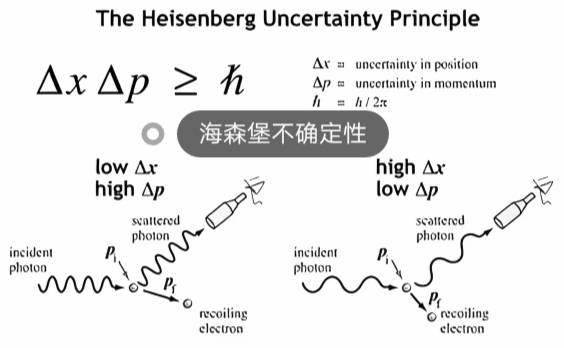
    量子力学的粒子具有波粒二象性，即它们既表现出粒子的特性，也表现出波的特性。
    • 当粒子表现为波时，
      
      它的位置和动量就像波的波峰和波长原生"模糊", 因此无法同时测量得非常精确。

• 与经典物理学的区别：

  • 在经典物理学，物体的运动可以通过精确测量其位置和动量来完全描述。
  • 在量子力学，存在的不确定性原理, 即使在同一时刻, 也无法同时精确地测得粒子的所有特征。
    
    这与经典物理学的确定性观点不同，强调了量子世界的随机性和概率性。

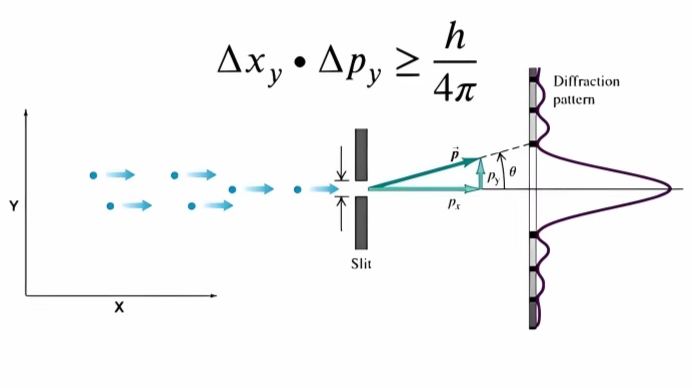
解释实例: 位置与动量 的关系

• 假设你正在测量一个电子的位置。
  
  由于量子效应，电子的位置并不是一个确定的点，而是有一定的概率分布。
  • 如果你希望把 "电子的位置"测量得非常精确，
    
    这意味着你需要提高测量精度，使得电子在某个位置出现的概率变得更为密集。
    
    但是电子有原生的波动性，这种"精确定位"会导致电子的动量变得非常不确定。
    
    即 你无法知道它的速度和方向。
  • 如果你希望精确测量电子的动量，同理，你就无法知道它的确切位置。
  • 根本原因是因为 "粒子的波动性" 使得 "它的运动状态" 总有一定的不确定性(模糊性)。
• 为什么会有这种不确定性？
  
  不确定性原理的根本原因与量子力学的波动性密切相关。
  
  量子粒子（如电子）既有粒子性，也有波动性。
  
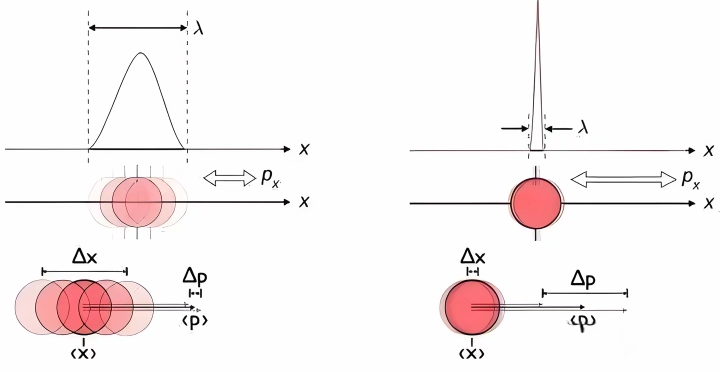
  粒子的位置和动量实际上是通过它的波函数描述，而波函数在空间的分布本身是模糊的。
  
  因此，我们不能用经典物理的精确值来描述粒子的位置和动量，而只能通过概率分布来描述它们的行为。
• 波函数 描述 量子粒子的动量:
  
  在量子力学，粒子的位置和动量都可以用波函数（(,)ψ(x,t)）来表示。
  
  "波函数的平方"给出粒子在某一位置出现的'概率密度'，但这个概率密度是扩展的，
  
  因而无法精确给出位置和动量的确切数值。

不确定性原理的深远影响

• 量子力学的非经典性：
  
  海森堡不确定性原理表明，量子力学与经典物理学的根本区别。
  
  经典物理学是基于确定性规律的，
  
  即如果我们知道一个物体的初始状态（位置和动量），就可以精确预测它的未来运动。
  
  而量子力学则是基于概率性的，它无法给出粒子确切的状态，而只能给出某些事实的概率。
• 量子隧穿效应：
  
  "量子隧穿" 是量子力学的一个奇特现象，它允许粒子穿越经典物理学认为不可能跨越的势垒。
  
  由于不确定性原理，粒子的位置和动量不可能同时精确确定，
  
  因此粒子有一定的概率“穿透”能量障碍，即使这种行为是在经典物理不可能的。
• 量子测量问题：
  
  不确定性原理与量子测量问题密切相关。
  
  量子力学表明，粒子的状态是通过波函数表示的，而波函数在观测之前是处于一种叠加状态。
  
  一旦进行测量，波函数“坍缩”到某个高度确定状态。
  
  这种过程并非完全精确，而是带有一定的不确定性。

量子技术

不确定性原理是量子计算、量子通信和量子加密等技术的基础。

例如，量子计算机的运作利用到“量子叠加和纠缠”等量子效应，

这些现象本身也与量子力学的不确定性密切相关。

实际应用

• 电子显微镜：
  
  电子显微镜通过使用电子束来成像，
  
  由于电子原生有波动性，它们的行为符合不确定性原理。
  
  尽管如此，电子显微镜仍然能够达到非常高的分辨率，
  
  这是因为电子波的波长比光波的短，才能够成像更小尺度的细节。
• 量子加密：
  
  量子通信 和 量子加密 基于 量子力学的不确定性原理。
  
  比如，QKD（量子密钥分发) 技术利用 量子力学的测量干扰效应 确保通信过程的安全性:
  
  任何第三方的窃听都会改变量子状态，在接收/解密过程的检测时就能被发现。