多校A层冲刺NOIP2024模拟赛18

T1 选彩笔（rgb）

签到题，但是没签上。。。

没想到三维前缀和，直接上了个bitset。

就是直接二分答案，然后枚举这三维每维的区间的起点，前缀和查数量是否大于等于 $ K $ 即可，也可以把二分答案改为第一维的双指针，少一个 $ log $ 。

T2 兵蚁排序（sort）

比T1还签到，但是没写 freopen 挂 100。

从 $ b $ 数组里挨个去在 $ a $ 数组里匹配，然后 $ O(n) $ 拉过来就行。

T3 人口局 DBA（dba）

数学推式子。

但是有很多部分分的数位DP，骗了 97 分。

简单来说就是解一个方程满足 $ x_1 + x_2 + x_3 + ······ + x_{n-1} + x_{n} = sum , x1 \lt p , \forall \ \ i ∈ [1,n] \ \ 0 \le x_i \lt m $ 的解的个数。

首先不考虑 $ x1 \lt p $ 的限制，然后你就可以容斥，钦定有 $ k $ 个 $ x $ 是大于 $ m $ 的，把他们斥掉，然后就有一个式子（直接插板）：

\[f_{a,s} \sum_{k=0}^{a} (-1)^k \binom{a}{k} \binom{s-km+a-1}{a-1}
\]

如果考虑上 $ x1 \lt p $ 的限制，那就可以直接枚举 $ x1 $ ，所以有：

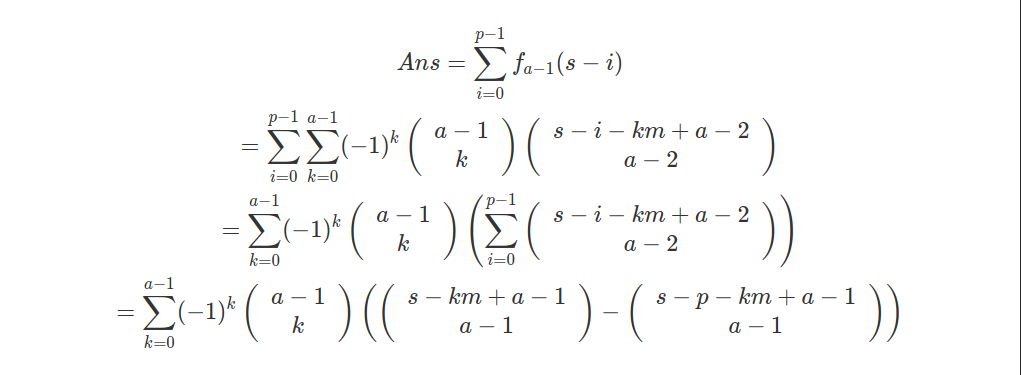
那个后面求和式的化简就是因为组合数的下面那个不变，所以在杨辉三角上就是竖着的一列

如图：

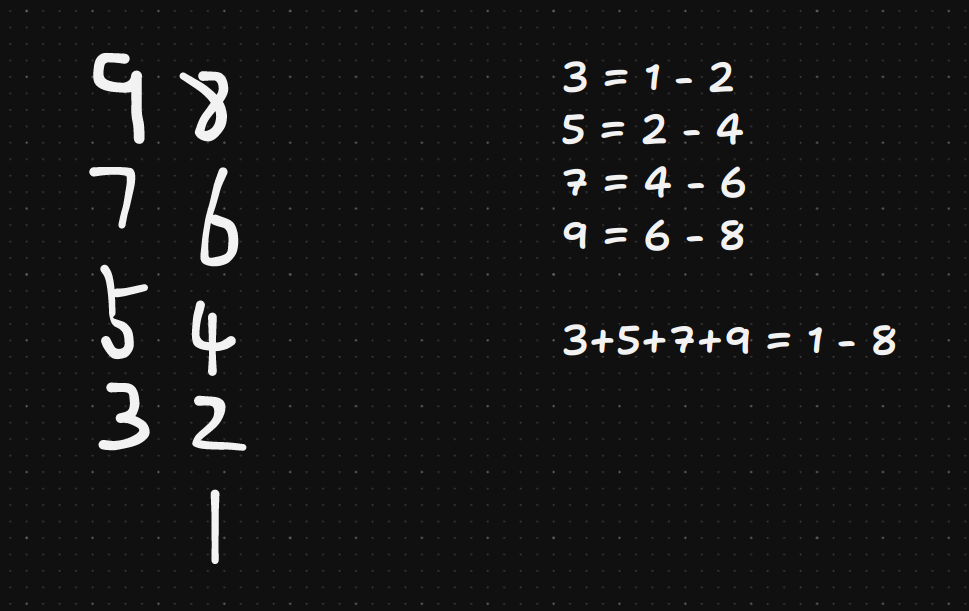
T4 银行的源起（banking）

因为讲过了，所以这篇讲的简单点。算了，还是稍微详细点吧。

首先考虑只有一个银行的时候怎么求，那肯定是所有人都往一个银行跑，所以枚举点然后算贡献？

其实这种题有 $ O (n) $ 做法。

首先以 1 为根，我们直接考虑每条边的贡献，对于一条边，他的权值是 $ w $ ，连接着点 $ j $ 和他的父亲 $ fa_j $ 。

对于这条边，要么是 $ j $ 和他的子树里面的点往上走经过这条边，要么是上面的点下来，这时候我们设 $ sz_j $ 是 $ j $ 及其子树里面的点的权值之和， $ tot $ 表示整棵树的权值和，直接取 $ w \times \min( sz_j , tot - sz_j) $ ，作为这条边的贡献即可。

为什么对，来证明一下：

上面的式子只能保证对于一条边来说是最优的，但是不能保证全局都是这样的，但其实全局最优可以被证明只有在每个都最优的时候才成立。

证毕。此时我们得到了 $ O(n) $ 解决一个银行的问题的方法。那如果有两个银行呢，这个时候也一定存在一条边没有人走，所以我们枚举一条边并把它断开，然后对于两棵树分别求贡献加和，即可 $ O(n^2) $ 解决。

$ O(n^2) $ 解决不了，那就看看能不能上数据结构优化。

优化肯定要从贡献方面入手，那就再看看那个贡献的式子， $ ans_j = w_j \times \min( sz_j , tot - sz_j ) $ ，这个 min 就很难直接优化，那就分讨，如果 $ sz_j \le \frac{tot}{2} , ans_j = w_j \times sz_j $ ，否则 $ ans_j = w_j \times (tot - sz_j ) $ ，那么这东西可以上值域线段树，具体来说，对于 $ sz $ 开一颗值域线段树，然后维护好 $ \sum w_j 、 \sum w_j \times sz_j $ 然后就可以做了。

主体思路有了，具体的分析一下：

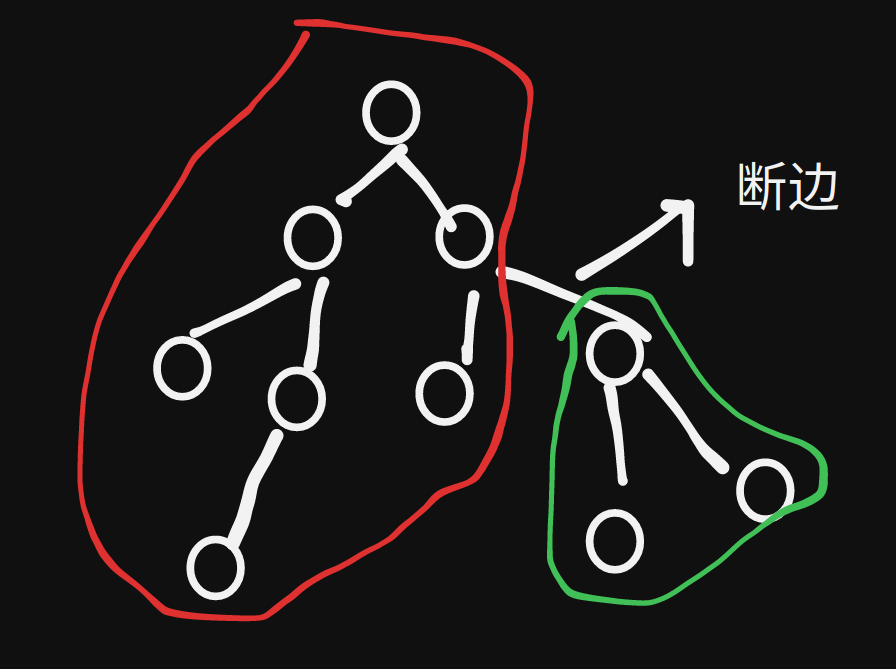
在这个图里面，我们将这棵树分成了两部分，一颗红的，一颗绿的，我们分别求贡献。

对于绿色的部分很好求，就用刚才的至于线段树就行，dfs时线段树合并 $ n( log (n) ) $ ，对于红色的部分稍微麻烦一点。

首先考虑红色的部分相对于原树有哪些变化：

红树的 $ tot = sz_1 - sz_j $

对于绿树中的根 $ j $ ，从他的父亲 $ x $ 到 1 的这条链上面的点 $ i $ ， $ sz_i $ 都减少了 $ sz_j $ 。

首先链上的点的贡献肯定得单求，可以维护一颗树状数组，然后每次查询时先链减，然后问，但是一个技巧可以不用链减，现在的分讨条件是 $ sz_i - sz_j \le \frac{tot}{2} $ ，那么直接移项，分讨条件变为 $ sz_i \le \frac{tot}{2} + sz_j $ ，同时最后求的答案要用减去 $ sz_j $ 之后的值。（写出式子来就会了）

接下来就是红树中除了链上的部分了，我们发现这部分很难直接求，线段树也不好维护，但是他就是全局除了链上和绿树上以外的所有点，所以我们求出全局对于 $ \frac{tot}{2} $ 的贡献，这部分可以弄一颗静态的全局线段树，也可以直接离散化后前缀和，然后减去链上以及绿树中对于 $ \frac{tot}{2} $ 的贡献即可，这部分都可以用刚才维护的东西直接求。

那我们就求完了，这道题主要是多注意注意细节就行了。