【树形dp】7.14城市

很典型的按照边考虑贡献的题。

题目描述

小A居住的城市可以认为由n个街区组成。街区从1到n依次标号街区与街区之间由街道相连，每个街区都可以通过若干条街道到达任意一个街区，共有n-1条街道。其中标号为i的街区居住了i名居民。居民会去拜访别人，但是要花费dis(u,v)的过路费，u是他所在的城市，v是他拜访的人所在的城市。你需要求出，所有人都拜访其他人一次花费的过路费之和。

输入格式

第一行一个整数nn接下来n-1行,每行2个整数n−1n−1个整数描述n-1条街道

输出格式

一个整数，表示总花费之和

样例输入

5

1 2

2 3

2 4

1 5

样例输出

184

数据规模与约定

对于30%的数据，满足n≤200n≤200

对于60%的数据，满足n≤3000n≤3000

对于100%的数据，满足n≤1000000n≤1000000

---

题目分析

是一道典型的按边统计答案的题。但为什么我又没想出来啊。

题目求的是∑u∑v∗dis(u,v)，那么来考虑一下问题的瓶颈在哪里。

按照定义直接做

首先是按照定义直接做的想法。

那么统计枚举所有点对，是 O(n^2) 的，预处理 dis(u,v) 有 O(n^3) 的floyd；还有 O(n^2) 的做 n 次dfs。

然而这个方向的做法空间复杂度是肯定要 O(n^2) 的，而且统计枚举的复杂度也难以改进。

考试时候就是吊死在这颗树上没出来了……

分边考虑贡献

统计时候不要那么“直接”，而是把整个答案分部分来考虑。

对于每一个点，与之相关的答案是 i*∑dis[i] 。于是我们发现最后的答案是只与 sum_{dis_i} 有关的。也就是说，对于点 x ，如果预处理了以它为根的 dis[] ，那么其贡献就是可以 O(1) 求出的。因此，解题瓶颈从处理点对的 dis[u][v] 变为了转移 dis[i] 。

对此，Cptraser表示有一种神奇的“平衡移动”方法。

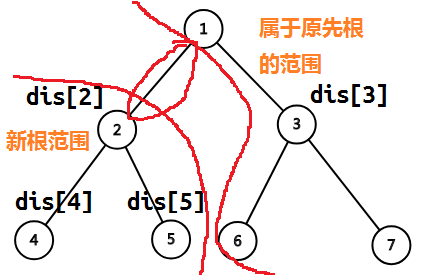
这里(1,2)这条边是正在枚举的边。我们现在要做的是快速将 ∑dis[](以1为根) 转为 ∑dis[](以2为根) 。

图画出来后就很显然了。有$\sum_{newDis[]} \qquad \quad =\sum_{dis[]} \quad +tot_v-2*size[v]$ 。其中 size[v] 表示以 v 为根子树大小。当然这里所谓的子树大小是要提前人为确定一个根节点的。

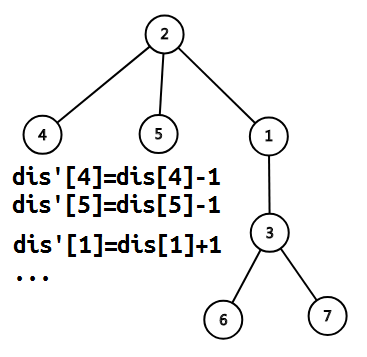
这般把答案分部分之后，我们就会惊喜地发现复杂度降为$O(n+m)$了。

 #include<bits/stdc++.h>
 typedef long long ll;
 const ll MO = 1e9+;
 const int maxn = ;
 const int maxm = ;

 int n;
 int edges[maxm],nxt[maxm],head[maxn],edgeTot;
 ll tmp,ans,sum,dis[maxn],size[maxn];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 void addedge(int u, int v)
 {
     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
     edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;
 }
 void dfs1(int x, int fa)
 {
     size[x] = x;
     for (int i=head[x]; i!=-; i=nxt[i])
         if (edges[i]!=fa)
              dis[edges[i]] = dis[x]+, dfs1(edges[i], x), size[x] += size[edges[i]];
 }
 void dfs2(int x, int fa)
 {
     ll cnt = ;
     for (int i=head[x]; i!=-; i=nxt[i])
         if (edges[i]!=fa){
             int v = edges[i];
             cnt = (sum-2ll*size[v])%MO;
             tmp = (tmp+cnt)%MO;
             ans = (ans+tmp*v%MO)%MO;
             dfs2(v, x);
             tmp = (tmp-cnt+MO)%MO;
         }
 }
 ll qmi(ll a, ll b)
 {
     ll ret = ;
     while (b)
     {
         if (b&) ret = ret*a%MO;
         a = a*a%MO, b >>= ;
     }
     return ret;
 }
 int main()
 {
     memset(head, -, sizeof head);
 //    freopen("city.in","r",stdin);
 //    freopen("city.out","w",stdout);
     n = read();
     for (int i=; i<n; i++) addedge(read(), read());
     dfs1(, );
     for (int i=; i<=n; i++) tmp += 1ll*i*dis[i];
     ans = tmp, sum = 1ll*(n+)*n/;
     dfs2(, );
     printf("%lld\n",ans*qmi(, MO-)%MO);
     return ;
 }

END