codeforces 569D D. Symmetric and Transitive(bell数+dp)

题目链接：

D. Symmetric and Transitive

time limit per test

1.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Johnny has recently learned about set theory. Now he is studying binary relations. You've probably heard the term "equivalence relation". These relations are very important in many areas of mathematics. For example, the equality of the two numbers is an equivalence relation.

A set ρ of pairs (a, b) of elements of some set A is called a binary relation on set A. For two elements a and b of the set A we say that they are in relation ρ, if pair 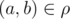, in this case we use a notation .

Binary relation is equivalence relation, if:

1. It is reflexive (for any a it is true that );
2. It is symmetric (for any a, b it is true that if , then );
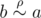3. It is transitive (if  and 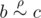, than ).

Little Johnny is not completely a fool and he noticed that the first condition is not necessary! Here is his "proof":

Take any two elements, a and b. If , then 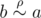 (according to property (2)), which means  (according to property (3)).

It's very simple, isn't it? However, you noticed that Johnny's "proof" is wrong, and decided to show him a lot of examples that prove him wrong.

Here's your task: count the number of binary relations over a set of size n such that they are symmetric, transitive, but not an equivalence relations (i.e. they are not reflexive).

Since their number may be very large (not 0, according to Little Johnny), print the remainder of integer division of this number by10^9 + 7.

Input

A single line contains a single integer n (1 ≤ n ≤ 4000).

Output

In a single line print the answer to the problem modulo 10^9 + 7.

Examples

input

1

output

1

input

2

output

3

input

3

output

10

Note

If n = 1 there is only one such relation — an empty one, i.e. 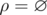. In other words, for a single element x of set A the following is hold: .

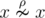If n = 2 there are three such relations. Let's assume that set A consists of two elements, x and y. Then the valid relations are 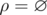,ρ = {(x, x)}, ρ = {(y, y)}. It is easy to see that the three listed binary relations are symmetric and transitive relations, but they are not equivalence relations.

题意：

问有n个元素,一共可以组成多少个有对称性和传递性但没有自反性的集合;

思路：

bell数,用递推公式加dp解决;

AC代码：

/*2014300227    569D - 21    GNU C++11    Accepted    62 ms    62692 KB*/
#include <bits/stdc++.h>
using namespace std;
const int N=12e5+;

typedef long long ll;
const ll mod=1e9+;
const double PI=acos(-1.0);
int dp[][];
int main()
{
    int n;
    scanf("%d",&n);

    dp[][]=;
    for(int i=;i<=n;i++)
    {

        dp[i][]=dp[i-][i-];
        for(int j=;j<=n;j++)
        {
            dp[i][j]=(dp[i][j-]+dp[i-][j-])%mod;
        }
    }
    ll ans=;
    for(int i=;i<=n;i++)
    {
        ans+=dp[n][i];
        ans%=mod;
    }
    cout<<ans<<"\n";

    return ;
}