编译原理-NFA构造DFA

本题摘自北邮的编译原理与技术。

首先，根据此图构造状态转换表

表中第一列第一行表示从第一个符号B通过任意个空转换能到达的节点，Ia表示由此行的状态数组（{B，5，1}可以看作0状态）经过一个a可以到达的节点，同理，Ib表示由状态数组经过一个b可以到达的节点。

当然，有些人可能觉得{B，5，1}和{5，1，3}看作两个状态不合理，他们之间不是有交集嘛，实际上他们之间并无交集，因为输入a后，{B，5，1}能到达的新节点是3，之所以要写成{5，1，3}，可能是要兼顾逻辑吧>_>

再仔细观察第一行，既然第一列可以看作一个状态，那么第二列就可以看作首状态输入一个a到达的另一个状态，所以可以把剩下两个{5，1，3}和{5，1，4}放入二三行的第一列作为状态1和状态2，简而言之，就是几个不同状态之间通过输入a，b来达到另一个状态。（不知道我用自己的理解来讲有没有讲清楚。。。）重复的状态数组自然是略过，毕竟这个表格是为了穷举所有状态之间关系，因此第四行第一个是{5，1，3，2，6，E}。

因此，根据此状态转换表，可以进一步得到下表

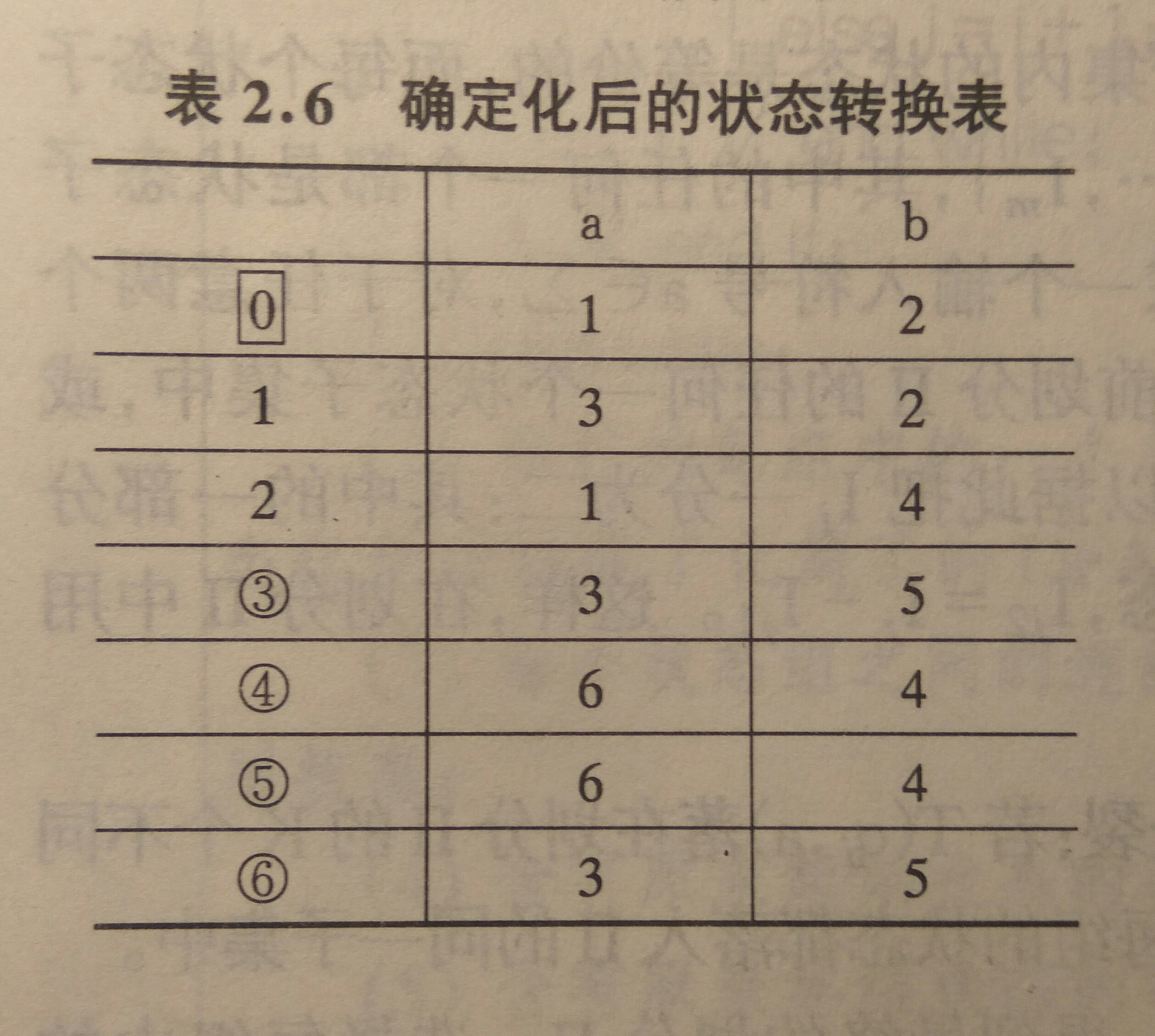
由于E是终结状态，因此，包含E的状态都是终结状态，3，4，5，6均为终结状态。

接下来画状态转换图就不必多说了吧。

请无视我模糊到变形的图片，能看清楚就好

参考文章：NFA转变为DFA