04-树6. Huffman Codes--优先队列（堆）在哈夫曼树与哈夫曼编码上的应用

题目来源：http://www.patest.cn/contests/mooc-ds/04-%E6%A0%916

In 1953, David A. Huffman published his paper "A Method for the Construction of Minimum-Redundancy Codes", and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encountering a big problem: the Huffman codes are NOT unique. For example, given a string "aaaxuaxz", we can observe that the frequencies of the characters 'a', 'x', 'u' and 'z' are 4, 2, 1 and 1, respectively. We may either encode the symbols as {'a'=0, 'x'=10, 'u'=110, 'z'=111}, or in another way as {'a'=1, 'x'=01, 'u'=001, 'z'=000}, both compress the string into 14 bits. Another set of code can be given as {'a'=0, 'x'=11, 'u'=100, 'z'=101}, but {'a'=0, 'x'=01, 'u'=011, 'z'=001} is NOT correct since "aaaxuaxz" and "aazuaxax" can both be decoded from the code 00001011001001. The students are submitting all kinds of codes, and I need a computer program to help me determine which ones are correct and which ones are not.

Input Specification:

Each input file contains one test case. For each case, the first line gives an integer N (2 <= N <= 63), then followed by a line that contains all the N distinct characters and their frequencies in the following format:

c[1] f[1] c[2] f[2] ... c[N] f[N]

where c[i] is a character chosen from {'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}, and f[i] is the frequency of c[i] and is an integer no more than 1000. The next line gives a positive integer M (<=1000), then followed by M student submissions. Each student submission consists of N lines, each in the format:

c[i] code[i]

where c[i] is the i-th character and code[i] is a string of '0's and '1's.

Output Specification:

For each test case, print in each line either “Yes” if the student’s submission is correct, or “No” if not.

Sample Input:

7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11

Sample Output:

Yes
Yes
No
No

题目大意：通过给定的字符及其访问次数，判断给定的编码是否为哈夫曼编码
判断条件：满足条件的编码形成的哈夫曼树可能不同，但其带权路径长度WPL一定相同且最小；且满足前缀码（前缀码是任何字符的编码都不是另一字符编码的前缀，前缀码可以避免二义性）
解题思路：
    1.根据输入的节点(字符)以及权重(访问次数),模拟建立哈夫曼树，并求出其WPL
        a.把权重建成一个最小堆（数组实现），然后每次弹出最小堆的最小元素即根节点
        b.构造一个新的节点：从堆中依次弹出两个最小的元素的和作为新节点的权重，再将新节点插入堆中
        c.WPL的值就是所有新节点的权重的和
    2.根据输入的编码计算WPL用来判断是否与哈夫曼树的WPL相同
        WPL等于每个字符编码访问次数与编码长度的乘积之和
    3.根据输入的编码判断是否为前缀码
        双重循环遍历，判断两个字符中某一个字符编码是否是另一个字符编码的前缀

图解建立哈夫曼树的过程中最小堆与哈夫曼树的变化如下：

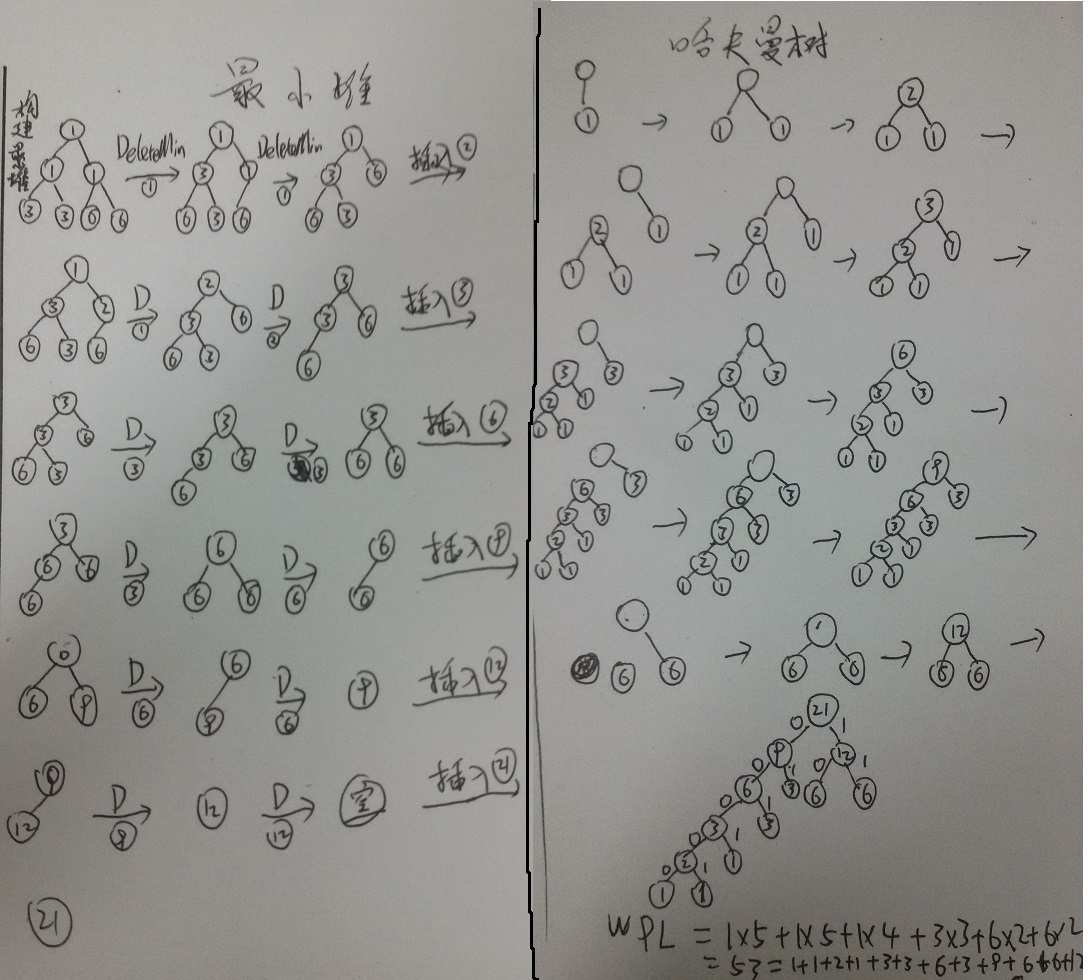
代码如下：

#include <cstdio>
#include <cstdlib>
#include <cctype>
#include <cstring>

#define N 64        //最大字符数
#define M 200       //最大编码长度

int HuffmanWPL(int heap[]);                             /*模拟建立哈夫曼树，返回WPL*/
void PercolateDown(int heap[], int *Size, int parent);  /*从节点parent开始下滤*/
void BuildMinHeap(int heap[], int *Size);               /*通过传入的完全二叉树（数组）建立最小堆*/
int DeleteMin(int heap[], int *Size);                   /*删除堆中最小元素 */
void Insert(int minHeap[], int * Size, int weight);     /*向最小堆中插入权重为weight的节点*/
int CountWPL(int f[], char code[][M]);                  /*计算一种编码的WPL*/
bool IsPrefixcode(char code[][M]);                      /*判断某种编码是否为前缀码*/
bool IsPrefix(char *s1, char *s2);                      /*判断两个字符中某一个字符编码是否是另一个字符编码的前缀*/

int n;      //全局变量，字符的个数

int main()
{
    char ch, code[N][M];
    int f[N];
    scanf("%d", &n);
    for (int i = ; i <= n; i++) {
        while(ch = getchar()) {
            if (isalpha(ch) || isdigit(ch) || ch == '_') {    //如果是字符
                scanf("%d", &f[i]);         //输出对应的访问次数
                break;
            }
        }
    }
    int minWPL = HuffmanWPL(f);             //通过模拟哈夫曼树得到最小WPL

    int stusNum;                            //学生个数（编码种类）
    scanf("%d", &stusNum);
    for (int i = ; i < stusNum; i++) {
        for (int j = ; j <= n; j++) {
            while(ch = getchar()) {
                if (isalpha(ch) || isdigit(ch) || ch == '_') {    //若为字符
                    scanf("%s", code[j]);                         //输入对应字符的编码
                    break;
                }
            }
        }
        int thisWPL = CountWPL(f, code);
        if (thisWPL == minWPL && IsPrefixcode(code))    //若WPL为最小且为前缀码
            printf("Yes\n");
        else
            printf("No\n");
    }
    return ;
}

bool IsPrefixcode(char code[][M])
{
    for (int i = ; i <= n; i++)
        for (int j = i+; j <= n; j++)
            if (IsPrefix(code[i], code[j]))
                return false;
    return true;
}

bool IsPrefix(char *s1, char *s2)
{
    while (s1 && s2 && *s1 == *s2) {  //从编码首位向后遍历,当遍历到末端或两者不相等时退出循环
        s1++;
        s2++;
    }
    if (*s1 == '\0' || *s2 == '\0')   //若遍历到某个字符编码的末端
        return true;                  //则该字符是另一字符的前缀
    else
        return false;
}

int CountWPL(int f[], char code[][M])
{
    int WPL = ;
    for (int i = ; i <= n; i++)
        WPL += f[i] * strlen(code[i]);  //权重*编码长
    return WPL;
}

void PercolateDown(int heap[], int *Size, int parent)
{
    int temp = heap[parent];
    int i, child;

    for (i = parent; i* <= (*Size); i = child){
        child =  * i;
        if (child != (*Size) && heap[child+] < heap[child])    //找到值更小的儿子
            child++;
        if (temp > heap[child])     //如果值比下一层的大
            heap[i] = heap[child];  //下滤
        else
            break;
    }
    heap[i] = temp;
}

void BuildMinHeap(int heap[], int *Size)
{
    for (int i = (*Size) / ; i > ; i--)   //从最后一个有儿子的节点开始
        PercolateDown(heap, Size, i);       //向前构造最小堆
}

int DeleteMin(int heap[], int *Size)
{
    int minElem = heap[];          //最小堆根节点为最小值
    heap[] = heap[*Size];          //将最小堆最后一个节点放到根节点处
    (*Size)--;                      //节点数减一
    PercolateDown(heap, Size, );   //从根节点开始下滤
    return minElem;
}

void Insert(int heap[], int * Size, int weight)
{
    int i;
    for (i = ++(*Size); i >  && heap[i/] > weight; i /= )    //先将要插入的节点放最后
        heap[i] = heap[i/];                                    //再上滤
    heap[i] = weight;
}

int HuffmanWPL(int heap[])
{
    int minHeap[N];
    int Size = ;

    for (int i = ; i < n; i++)
        minHeap[Size++] = heap[i];  //将构造最小堆的数组初始化
    minHeap[Size] = heap[n];
    BuildMinHeap(minHeap, &Size);

    int WPL = ;
    for (int i = ; i < n; i++) {
        int leftWeight = DeleteMin(minHeap, &Size);
        int rightWeight = DeleteMin(minHeap, &Size);
        int rootWeight = leftWeight + rightWeight;
        WPL += rootWeight;
        Insert(minHeap, &Size, rootWeight);
    }
    return WPL;
}