图的DFS与BFS遍历

一、图的基本概念

1、邻接点：对于无向图无v₁ 与v₂之间有一条弧，则称v1与v2互为邻接点；对于有向图而言<v₁,v₂>代表有一条从v₁到v₂的弧，则称v₂为v₁的邻接点。

2、度：就是与该顶点相互关联的弧的个数。

3、连通图：无向图的每个顶点之间都有可达路径，则称该无向图为连通图。有向图每个顶点之间都有<v₁,v₂>和<v₂,v₁>，则称此有向图为强连通图。

二、存储结构

1、邻接矩阵存储（Adjacency Matrix）

对无权图，顶点之间有弧标1，无弧标0；

对有权图，顶点之间有弧标权，无弧标无穷大；

2、邻接表（看书吧，精力有限不想画图了）

三、DFS与BFS

其实深度优先和广度优先，最重要的是要掌握其思想，而不是具体的实现，因为万变不离其宗。

1、DFS深度优先

①从v0出发访问v0

②找到刚访问过得顶点，访问其未访问过得邻接点中的一个。重复②直到不再有邻接点位置。

③回溯，返回前一个被访问过但是仍有未被访问过得邻接点的顶点，继续访问它的下一个邻接点。重复②直至完全遍历。

可能我描述的不够准确，但那也没有办法，应为有些东西真的是只能意会。学计算机必须要结合具体的例子来看。

原图：

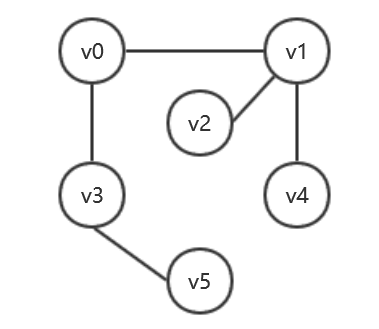
DFS

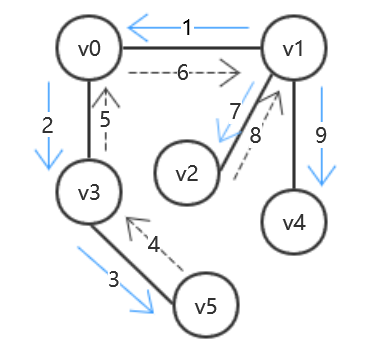
其实简单来说：就是如果访问到的结点有邻接点就一直向下访问，否则就回溯。同树中的先根遍历很类似。

数据存储结构：

String[] vertex = new String[] {"v0","v1","v2","v3","v4","v5"};
int[][] matrix  = new int[][] {
        {0,1,0,1,0,0},
        {1,0,1,0,1,0},
        {0,1,0,0,0,0},
        {1,0,0,0,0,1},
        {0,1,0,0,0,0},
        {0,0,0,1,0,0}
};
int[] visited = new int[6];//标记访问过得结点

递归实现：

void matrixDFS(int v0) {
    System.out.print(vertex[v0] + " ");
    visited[v0] = 1;
    //遍历寻找v0的邻接点
    for(int i = 0; i < vertex.length; i++) {
        if(matrix[v0][i] == 1 && visited[i] == 0) {
            matrixDFS(i);
        }
    }
}

非递归实现：

//基于栈的非递归实现
void matrixDFS1(int v0) {
    Stack<Integer> stack = new Stack<Integer>();
    stack.push(v0);
    while(!stack.isEmpty()) {
        int v = stack.pop();
        if(visited[v] == 0) {//栈中很可能有重复的元素
            System.out.print(vertex[v] + " ");
            visited[v] = 1;
            for(int i = 0; i < matrix.length; i++) {
                if(matrix[v][i] == 1 && visited[i] == 0) {
                    stack.push(i);
                }
            }
        }
    }
}

 2、BFS深度优先遍历

①访问v0

②访问v0所以未被访问过的邻接点

③分别以这些邻接点（②中的邻接点）出发，去访问他们的邻接点。重复③知道遍历结束。

BFS就比较像树中的层次遍历

代码实现：

void matrixBFS2(int v0) {
    Queue<Integer> queue = new LinkedList<>();
    queue.offer(v0);
    while(!queue.isEmpty()) {
        int v = queue.poll();
        if(visited[v] == 0) {
            System.out.print(vertex[v] + " ");
            visited[v] = 1;
            for(int i = 0; i < vertex.length; i++) {
                if(matrix[v][i] == 1 && visited[i] == 0) {
                    queue.offer(i);
                }
            }
        }
    }
}

可以看到这段代码和DFS递归实现的代码差别只是一个用栈一个用队列。

DFS：访问v0，邻接点如栈

BFS：访问v0，邻接点入队

我们的目标不是要掌握这些具体的实现，而是理解DFS与BFS算法的思想，将其活学活用。

数据结构与算法参考