bzoj 3996: [TJOI2015]线性代数

Description

给出一个N*N的矩阵B和一个1*N的矩阵C。求出一个1*N的01矩阵A.使得

D=（A*B-C）*A^T最大。其中A^T为A的转置。输出D

Input

第一行输入一个整数N，接下来N行输入B矩阵，第i行第J个数字代表Bij.

接下来一行输入N个整数，代表矩阵C。矩阵B和矩阵C中每个数字都是不超过1000的非负整数。

Output

输出最大的D

Sample Input

3
1 2 1
3 1 0
1 2 3
2 3 7

Sample Output

2

HINT

1<=N<=500

Source

经过推导得出：

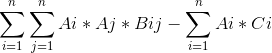
是一个最大权闭合子图的模型

选择一个Ai==1,会损失Ci;

对于一个点对(i,j),当Ai和Aj同时==1时,可以获得Bij的收益；

由于收益是同时依赖于两个点的，所以可以对每一个点对新建一个附加点tt,从s向其连Bij的边,然后tt向i,j连Inf;

其余的连边就是最大权闭合子图的套路了

最后正权和-最小割即为答案

(玄学剪枝真有用)

// MADE BY QT666
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
#define RG register
using namespace std;
typedef long long ll;
const int N=2000000;
const int Inf=19260817;
int gi()
{
  int x=0;
  char ch=getchar();
  while(ch<'0'||ch>'9') ch=getchar();
  while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
  return x;
}
int head[N],nxt[N],to[N],s[N],cnt=1,S,T,n,sum,q[N],level[N],vis[N],F,c[N];
int b[600][600],C[1000],tot;
inline void Addedge(int x,int y,int z) {
  to[++cnt]=y,s[cnt]=z,nxt[cnt]=head[x],head[x]=cnt;
}
inline void lnk(int x,int y,int z){
  Addedge(x,y,z);Addedge(y,x,0);
}
inline bool bfs(){
  for(RG int i=S;i<=T;i++) level[i]=0,vis[i]=0;
  int t=0,sum=1;
  q[0]=S,level[S]=1,vis[S]=1;
  while(t<sum){
      int now=q[t++];
      if(now==T) return 1;
      for(RG int i=head[now];i;i=nxt[i]){
      int y=to[i];
      if(level[y]==0&&s[i]){
          level[y]=level[now]+1;
          q[sum++]=y;
        }
    }
    }
  return 0;
}
inline int dfs(int now,int maxf){
  if(now==T) return maxf;
  int ret=0;
  for(RG int i=head[now];i;i=nxt[i]) {
    int y=to[i],f=s[i];
    if(level[y]==level[now]+1&&f) {
      int minn=min(maxf-ret,f);
      f=dfs(y,minn);
      s[i]-=f;
      s[i^1]+=f;ret+=f;
      if(ret==maxf) break;
    }
  }
  if(!ret) level[now]=0;
  return ret;
}
inline void Dinic(){
    while(bfs()) F+=dfs(S,Inf);
}
int main(){
    n=gi();
    for(RG int i=1;i<=n;i++)
    for(RG int j=1;j<=n;j++) b[i][j]=gi();
    for(RG int i=1;i<=n;i++) C[i]=gi(),tot+=C[i];
    S=0,T=n+n*n+1;int ans=0,tt=n;
    for(RG int i=1;i<=n;i++) lnk(i,T,C[i]);
    for(RG int i=1;i<=n;i++){
    for(RG int j=1;j<=n;j++){
        tt++;lnk(S,tt,b[i][j]);ans+=b[i][j];
        lnk(tt,i,Inf);lnk(tt,j,Inf);
    }
    }
    Dinic();printf("%d\n",ans-F);
    return 0;
}