深度学习入门教程UFLDL学习实验笔记一：稀疏自编码器

UFLDL即（unsupervised feature learning & deep learning）。这是斯坦福网站上的一篇经典教程。顾名思义，你将在这篇这篇文章中学习到无监督特征学习和深度学习的主要观点。

UFLDL全文出处在这：http://ufldl.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B，本文为本人原创，参考了UFLDL的教程，是我自己个人对于这一系列教程的理解以及自己的实验结果。非盈利性质网站转载请在文章开头处著名本文作者：77695，来源http://www.cnblogs.com/cj695/。盈利性质网站转载请与作者联系，联系方式在文章后面。如未联系，本人将通过一切可能且合法的途径追缴相应稿酬。请在转载时保留此声明。

神经网络

一个神经网络由一系列神经元组成，一个神经元由一系列参数x1，x2。。。及偏置量+1作为输入，将输入与对应权值W（与x1,x2。。。相乘），（与1相乘）相乘后求和，并将和放入激活函数，即可得到该神经元的输出。我们称这个神经元的输入－输出映射关系其实就是一个逻辑回归（logistic regression）

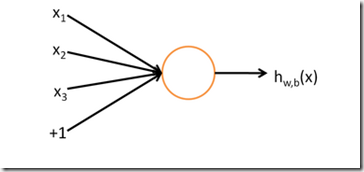
在这里激活函数我们用：

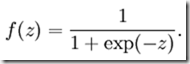他的导数是右边的形式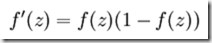

这是sigmoid函数的图像

整个神经元可以用一个公式表示：

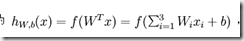
神经网络就是很多个神经元组合在一起，一个神经元的输出，也可以是另外一个神经元的输入，如下图：

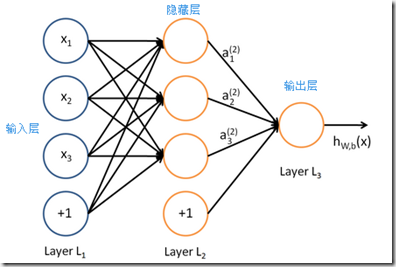
具体请直接查看UFLDL相应教程，这里不再赘述，下文一样。

反向传导算法

一个神经网络向前传导，其神经元的参数可以是各种各样的，这样也会导致各种各样的借，而我希望我整个神经网络的输出，是与我预期的输出越相近越好，为了描述相近的程度，我们计算神经网络输出与预计输出的差值的平方和。这个和越小，即输出与预期越接近，我们称这个叫做代价函数。但使得输出与预期接近的W参数组合有很多，并不是每一种组合都好，也不是说越接近越好，当W参数太大的时候，会发生过拟合，使得泛化能力不够，因此我们引入所有W的平方和，加入到代价函数中，我们称它叫惩罚项。我们使用梯度下降法，求得最优的W，b这就是机器学习的整个过程。梯度下降中，其实就是求得代价函数对W，b的偏导值。在计算偏导的时候，因为复合函数的求导法则：

可以看到，要求整个惩罚函数的导数首先就要计算从惩罚函数开始向后求导，具体公式这里就不贴了。

梯度检验

要检测自己反向传导得到的偏导函数是否正确，这里有一种简单粗暴的方法，就是梯度检验，通过对某一个参数加以及减一个较小的值的差除以2倍较小的值即可近似算出该点偏导值，因此可以用来检验偏导是否计算正确。但为什么我们不直接用这个计算代替求偏导函数，因为太慢了！

在这里我们用L-BFGS算法快速计算偏导数

自编码算法与稀疏性

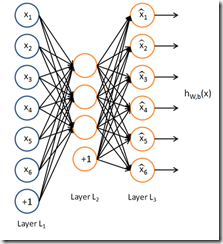
使得输出尽可能与输入一致我们称之为自编码。比如，若隐藏层神经元数目小于输入层，则这个网络就要学习怎么去压缩这些数据。使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。其惩罚函数如下：

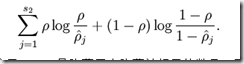
可视化自编码器训练结果

可以证明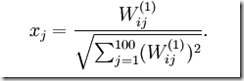，时有单元i有最大激励。

实现

生成数据集：即从所有10副512x512的图片中取8x8的块，一共取10000块。

这是数据集的一些图片，可以看到这主要是一些自然图片。

这里只粘贴所有自己实现部分的代码。

[w,h,n]=size(IMAGES);
randx=randi(w-patchsize,1,numpatches);
randy=randi(h-patchsize,1,numpatches);
randIdx=randi(n,1,numpatches);

for i=1 : numpatches
    pc=IMAGES(randx(i):randx(i)+patchsize-1,randy(i):randy(i)+patchsize-1,randIdx(i));
    patches(:,i)=pc(:);
end

生成结果如下：

实现惩罚函数以及梯度函数：按照之前的公式计算，大家直接看代码吧。

[l,n]=size(data);
dataHidden=sigmoid(W1*data+b1*ones(1,n));
dataOut=sigmoid(W2*dataHidden+b2*ones(1,n));
rou=sum(dataHidden,2)/n;
spCost=beta*(sum((sparsityParam*log(sparsityParam*ones(size(rou))./rou)...
    +(1-sparsityParam)*log(((1-sparsityParam)*ones(size(rou)))./(1-rou)))));
xyCost=(sum(sum((dataOut-data).*(dataOut-data))))/2/n;
wCost=(lambda/2)*((sum(sum(W1.*W1))+sum(sum(W2.*W2))));
cost=wCost+xyCost+spCost;
delta3=-(data-dataOut).*dataOut.*(1-dataOut);
spDt=beta*((-sparsityParam*ones(size(rou))./rou)+(((1-sparsityParam)...
    *ones(size(rou)))./(ones(size(rou))-rou)));
delta2=((W2')*delta3+spDt*ones(1,n)).*dataHidden.*(1-dataHidden);
W2grad=(delta3*(dataHidden'))/n+lambda*W2;
W1grad=(delta2*(data'))/n+lambda*W1;
b2grad=delta3*ones(n,1)/n;
b1grad=delta2*ones(n,1)/n;

实现时候出了一个问题，算梯度的时候少加了lambda*W1，粗心害死人啊！

梯度检验：按照公式实现梯度检验，检验实现的梯度是否正确。

for i=1 :(size(theta,1))
    e = zeros(size(theta));
    e(i)=EPSILON;
    cha=(J(theta+e)-J(theta-e));
    numgrad(i)=cha/(2*EPSILON);
end

看到运行结果

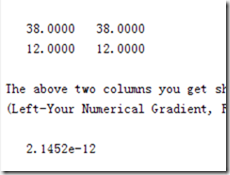
只差10^-12数量级，说明梯度检验的实现没错

训练以及结果：

最后运行得到结果如下：

可以看到学习出来的结果基本是图片相互正交的部分，相当于傅立叶变换中不同频率正弦波，相当于很多正交的基，这些“基”以一定的权重相加，就能够近似组成任何一个8x8的图片块。

另外值得一提的是，对于梯度下降算法，在这里使用的是L-BFGS算法，对于这个算法，我们不能将它用于商业用途，若用与商业用途的话，可以使用fminlbfgs函数，他比L-BFGS慢但可用于商业用途。