Adaptive gradient descent without descent

目录

• 概
• 主要内容
  • 算法1 AdGD
  • 定理1 ADGD-L
  • 算法2
  • 定理2
  • 算法3 ADGD-accel
  • 算法4 Adaptive SGD
  • 定理4
• 代码

Malitsky Y, Mishchenko K. Adaptive gradient descent without descent[J]. arXiv: Optimization and Control, 2019.

概

本文提出了一种自适应步长的梯度下降方法(以及多个变种方法), 并给了收敛性分析.

主要内容

主要问题:

\[\tag{1}
\min_x \: f(x).
\]

局部光滑的定义:

若可微函数\(f(x)\)在任意有界区域内光滑，即

\[\|\nabla f(x) - \nabla f(y)\| \le L_{\mathcal{C}} \|x-y\|, \quad \forall x, y \in \mathcal{C},
\]

其中\(\mathcal{C}\)有界.

本文的一个基本假设是函数\(f(x)\)凸且局部光滑.

算法1 AdGD

定理1 ADGD-L

定理1. 假设\(f: \mathbb{R}^d \rightarrow \mathbb{R}\) 为凸函数且局部光滑. 则由算法1生成的序列\((x^k)\)收敛到(1)的最优解, 且

\[f(\hat{x}^k) - f_* \le \frac{D}{2S_k} = \mathcal{O}(\frac{1}{k}),
\]

其中\(\hat{x}^k := \frac{\sum_{i=1}^k \lambda_i x^i + \lambda_1 \theta_1 x^1}{S_k}\), \(S_k:= \sum_{i=1}^k \lambda_i + \lambda_1 \theta\).

算法2

在\(L\)已知的情况下, 我们可以对算法1进行改进.

定理2

定理2 假设\(f\)凸且\(L\)光滑, 则由算法(2)生成的序列\((x^k)\)同样使得

\[f(\hat{x}^k)-f_*=\mathcal{O}(\frac{1}{k})
\]

成立.

算法3 ADGD-accel

这部分没有理论证明, 是作者基于Nesterov中的算法进行的改进.

算法4 Adaptive SGD

这个算法是对SGD的一个改进.

定理4

代码

\(f(x, y) = x^2+50y^2\), 起点为\((30, 15)\).

"""
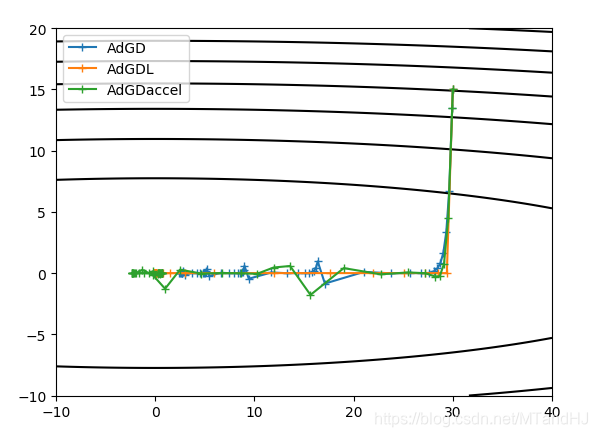
adgd.py
"""

import numpy as np
import matplotlib.pyplot as plt

State = "Test"

class FuncMissingError(Exception): pass
class StateNotMatchError(Exception): pass

class AdGD:

    def __init__(self, x0, stepsize0, grad, func=None):
        self.func_grad = grad
        self.func = func
        self.points = [x0]
        self.points.append(self.calc_one(x0, self.calc_grad(x0),
                                         stepsize0))
        self.prestepsize = stepsize0
        self.theta = None

    def calc_grad(self, x):
        self.pregrad = self.func_grad(x)
        return self.pregrad

    def calc_one(self, x, grad, stepsize):
        return x - stepsize * grad

    def calc_stepsize(self, grad, pregrad):
        part2 = (
            np.linalg.norm(self.points[-1]
                          - self.points[-2]) /
            (np.linalg.norm(grad - pregrad) * 2)

        )
        if not self.theta:
            return part2
        else:
            part1 = np.sqrt(self.theta + 1) * self.prestepsize
            return min(part1, part2)

    def update_theta(self, stepsize):
        self.theta = stepsize / self.prestepsize
        self.prestepsize = stepsize

    def step(self):
        pregrad = self.pregrad
        prex = self.points[-1]
        grad = self.calc_grad(prex)
        stepsize = self.calc_stepsize(grad, pregrad)
        nextx = self.calc_one(prex, grad, stepsize)
        self.points.append(nextx)
        self.update_theta(stepsize)

    def multi_steps(self, times):
        for k in range(times):
            self.step()

    def plot(self):
        if self.func is None:
            raise FloatingPointError("func is not defined...")
        if State != "Test":
            raise StateNotMatchError()
        xs = np.array(self.points)
        x = np.linspace(-40, 40, 1000)
        y = np.linspace(-20, 20, 500)
        fig, ax = plt.subplots()
        X, Y = np.meshgrid(x, y)
        ax.contour(X, Y, self.func([X, Y]), colors='black')
        ax.plot(xs[:, 0], xs[:, 1], "+-")
        plt.show()

class AdGDL(AdGD):

    def __init__(self, x0, L, grad, func=None):
        super(AdGDL, self).__init__(x0, 1 / L, grad, func)
        self.lipschitz = L

    def calc_stepsize(self, grad, pregrad):
        lk = (
            np.linalg.norm(grad - pregrad) /
            np.linalg.norm(self.points[-1]
                          - self.points[-2])
        )
        part2 = 1 / (self.prestepsize * self.lipschitz ** 2) \
                 + 1 / (2 * lk)
        if not self.theta:
            return part2
        else:
            part1 = np.sqrt(self.theta + 1) * self.prestepsize
            return min(part1, part2)

class AdGDaccel(AdGD):

    def __init__(self, x0, stepsize0, convex0, grad, func=None):
        super(AdGDaccel, self).__init__(x0, stepsize0, grad, func)
        self.preconvex = convex0
        self.Theta = None
        self.prey = self.points[-1]

    def calc_convex(self, grad, pregrad):
        part2 = (
            (np.linalg.norm(grad - pregrad) * 2) /
                np.linalg.norm(self.points[-1]
                        - self.points[-2])
        ) / 2
        if not self.Theta:
            return part2
        else:
            part1 = np.sqrt(self.Theta + 1) * self.preconvex
            return min(part1, part2)

    def calc_beta(self, stepsize, convex):
        part1 = 1 / stepsize
        part2 = convex
        return (part1 - part2) / (part1 + part2)

    def calc_more(self, y, beta):
        nextx = y + beta * (y - self.prey)
        self.prey = y
        return nextx

    def update_Theta(self, convex):
        self.Theta = convex / self.preconvex
        self.preconvex = convex

    def step(self):
        pregrad = self.pregrad
        prex = self.points[-1]
        grad = self.calc_grad(prex)
        stepsize = self.calc_stepsize(grad, pregrad)
        convex = self.calc_convex(grad, pregrad)
        beta = self.calc_beta(stepsize, convex)
        y = self.calc_one(prex, grad, stepsize)
        nextx = self.calc_more(y, beta)
        self.points.append(nextx)
        self.update_theta(stepsize)
        self.update_Theta(convex)

config.json:

{
  "AdGD": {
    "stepsize0": 0.001
  },
  "AdGDL": {
    "L": 100
  },
  "AdGDaccel": {
    "stepsize0": 0.001,
    "convex0": 2.0
  }
}

"""
测试代码
"""

import numpy as np
import matplotlib.pyplot as plt
import json
from adgd import AdGD, AdGDL, AdGDaccel

with open("config.json", encoding="utf-8") as f:
    configs = json.load(f)

partial_x = lambda x: 2 * x
partial_y = lambda y: 100 * y
grad = lambda x: np.array([partial_x(x[0]),
                              partial_y(x[1])])
func = lambda x: x[0] ** 2 + 50 * x[1] ** 2

fig, ax = plt.subplots()
x = np.linspace(-10, 40, 500)
y = np.linspace(-10, 20, 500)
X, Y = np.meshgrid(x, y)
ax.contour(X, Y, func([X, Y]), colors='black')

def process(methods, times=50):
    for method in methods:
        method.multi_steps(times)

def initial(methods, **kwargs):
    instances = []
    for method in methods:
        config = configs[method.__name__]
        config.update(kwargs)
        instances.append(method(**config))
    return instances

def plot(methods):
    for method in methods:
        xs = np.array(method.points)
        ax.plot(xs[:, 0], xs[:, 1], "+-", label=method.__class__.__name__)
    plt.legend()
    plt.show()

x0 = np.array([30., 15.])

methods = [AdGD, AdGDL, AdGDaccel]
instances = initial(methods, x0=x0, grad=grad, func=func)
process(instances)
plot(instances)