*衡树 Treap（树堆） 学习笔记

调了好几个月的 Treap 今天终于调通了，特意写篇博客来纪念一下。

0. Treap 的含义及用途

在算法竞赛中很多题目要使用二叉搜索树维护信息。然而毒瘤数据可能让二叉搜索树退化成链，这时就需要让二叉搜索树保持*衡，“*衡的”二叉搜索树自然就是“*衡树”啦。“Treap”就是*衡树的一种，由于它易学易写，所以在算法竞赛中很常用。

"Treap" 事英文单词 "Tree" 和 "Heap" 的合成词。顾名思义，它同时拥有树和堆的性质。Treap 每个节点维护两个权值 lev 和 val ,lev是随机分配的，满足堆（本文中指大根堆）性质，val 是 Treap 真正要存储的信息，满足二叉搜索树的性质。像这样：

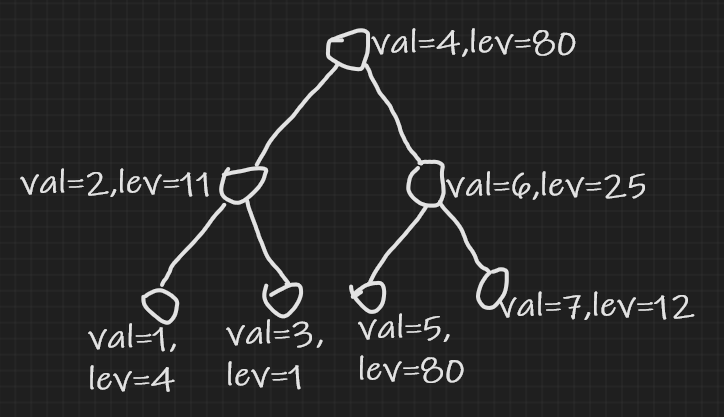
即节点的val值大于左儿子的val值小于右儿子的val值， lev值大于它的每个儿子的lev值。

这其实是一棵笛卡尔树。当笛卡尔树的两个权值都确定时，笛卡尔树的形态是唯一的。容易发现，二叉搜索树在数据随机时就是趋*于*衡的，而由于 Treap 的 lev 权值随机，也就是说 Treap 的形态随机，所以 Treap 的*衡也就有了保证。 好不靠谱啊（小声

下面博主将结合代码讲解 Treap。

1. 操作

1.-1. Treap 需要维护的信息

treap_node pool[MAXN+5];//内存池
struct treap_node{
    int ls,rs;//记录左右儿子节点编号
    int val;//treap要维护的信息
    int cnt/*treap内有多少个val，也就是val的副本数*/,siz/*当前子树大小*/,lev/*随机权值*/;
};
struct treap{
    int root;//存储树根
    treap(){
        root=nul;
    }
	void push_up(int p){//维护节点大小信息
        pool[p].siz=pool[pool[p].ls].siz+pool[pool[p].rs].siz+pool[p].cnt;
    }
}；

1.0. 新建节点、删除节点与垃圾回收

treap_node pool[MAXN+5];//内存池
int treap_tail;
const int nul=0;
queue<int> treap_rubbish;//“垃圾站”
int new_treap_node(){//新建节点
    int res=0;
    if(treap_rubbish.empty()){
        res=++treap_tail;
    }else{
        res=treap_rubbish.front();
        treap_rubbish.pop();
    }
    pool[res].cnt=pool[res].siz=pool[res].ls=pool[res].rs=0;
    pool[res].val=0;
    pool[res].lev=rand();
    return res;
}
void delete_treap_node(int &p){//删除节点
    treap_rubbish.push(p);//回收
    p=0;
}

博主在这里使用了一个辣鸡版的内存池。当删除节点时，可以把废旧的节点编号插入垃圾队列中，这样在下次新建节点时可以直接从垃圾队列里薅一个出来而不用新申请，可以在一定程度上节省空间。

1.1. 旋转

在 Treap 中，有时会出现 lev 的堆性质被破坏的现象，这时就需要用“旋转”操作来维护堆性质的同时不破坏二叉搜索树性质。例如这种情况：

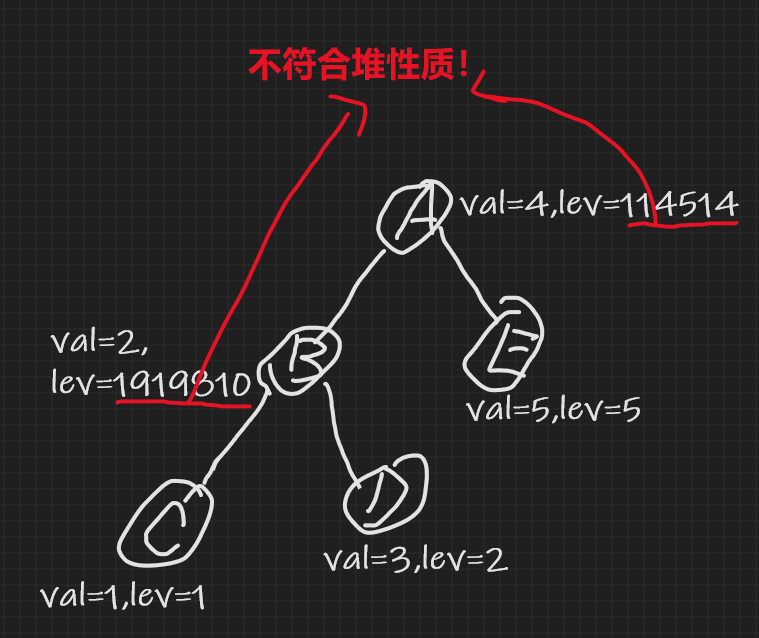
我们可以通过“左旋”来维护它。如图：

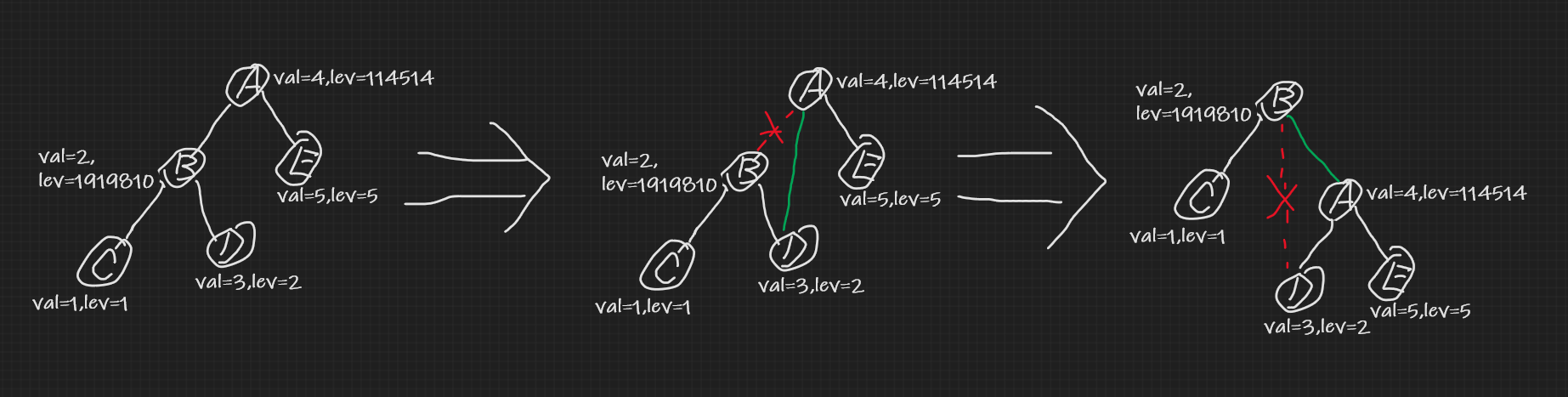
我们惊奇地发现，“左旋”操作在没有破坏二叉搜索树性质的前提下颠倒了节点A和节点B的父子关系！

“左旋”操作代码：

void zag(int &p){//由于此操作可能更改当前子树的根节点，所以要使用引用来确保p永远指向当前子树的根节点
    int tmp=pool[p].rs;
    pool[p].rs=pool[tmp].ls;
    pool[tmp].ls=p;
    push_up(p);push_up(tmp);
    p=tmp;
}

同样的，也存在一个右旋操作，代码如下：

void zig(int &p){
    int tmp=pool[p].ls;
    pool[p].ls=pool[tmp].rs;
    pool[tmp].rs=p;
    push_up(p);push_up(tmp);
    p=tmp;
}

容易发现，左旋和右旋是相反的操作。如图：

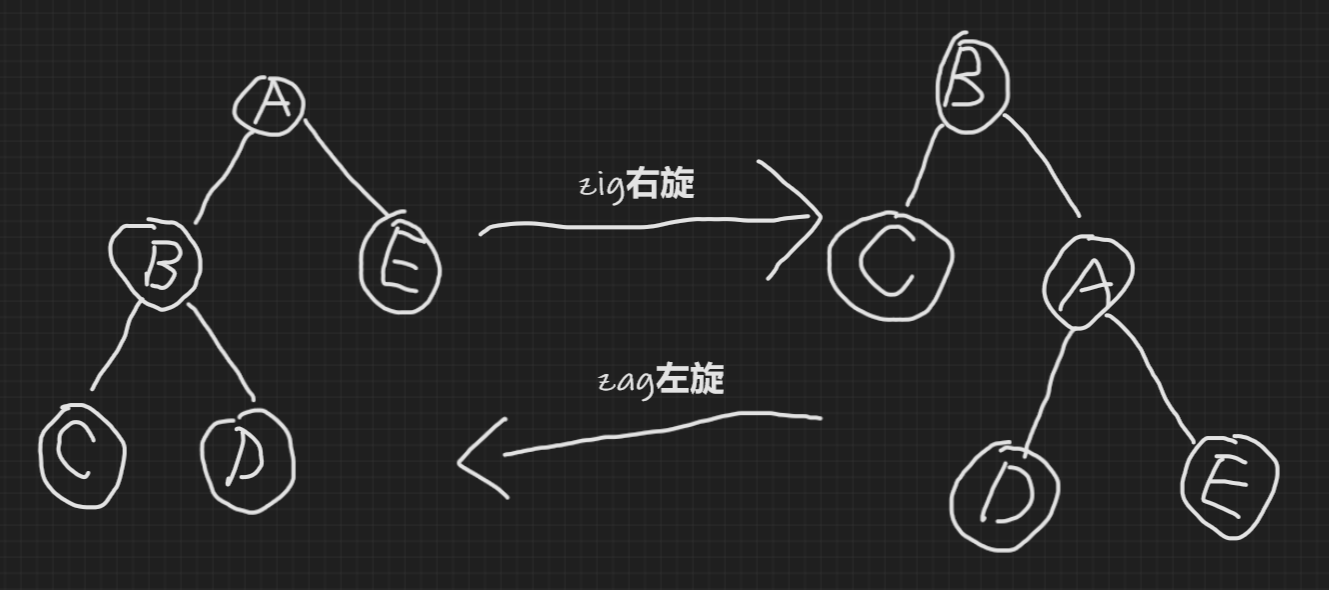
有了旋转操作，我们就可以在不破坏val的二叉搜索树性质的条件下维护lev的堆性质了。

有一个细节：由于旋转后当前子树的树根会改变，所以在zig和zag函数中参数p要传引用以方便修改p。

1.3. 插入与删除

Treap 的插入操作和普通二叉搜索树差不多，只不过如果在插入过程中堆性质被破坏要通过旋转来维护。代码如下：

void insert(int &p,int x){//插入
    if(p==nul){//如果没有值为x节点就新建一个
        p=new_treap_node();
        pool[p].val=x;
        pool[p].siz=pool[p].cnt=1;
    }else if(x==pool[p].val){//如果找到值为x节点就让副本数++
        pool[p].cnt++;
        push_up(p);
    }else if(x<pool[p].val){//递归
        insert(pool[p].ls,x);
        push_up(p);
        if(pool[pool[p].ls].lev>pool[p].lev)zig(p);//通过旋转维护lev的堆性质
    }else{//x>pool[p].val
        insert(pool[p].rs,x);
        push_up(p);
        if(pool[pool[p].rs].lev>pool[p].lev)zag(p);
    }
}

Treap 的删除操作稍微复杂亿点。由于 Treap 恶心的堆性质，所以在删除节点时要采取把节点旋转成叶子再直接删除的方式删除节点。

void erase(int &p,int x){
    if(p==nul){//没有值为x的节点就没有删除的必要了
    }else if(x==pool[p].val){//如果要删除当前节点
        if(pool[p].cnt>1){//如果有多个副本就副本数--
            pool[p].cnt--;push_up(p);
        }else{//如果只有1个副本就必须删除当前节点
            pool[p].cnt=0;
            if(!(pool[p].ls||pool[p].rs)){//如果当前节点是叶子就直接删除
                delete_treap_node(p);
            }else{//否则往下转
                //为满足堆性质要判断应该让左儿子还是右儿子“当爹”
                if(pool[p].rs==0||//只有左儿子
                (pool[p].ls&&pool[pool[p].ls].lev>pool[pool[p].rs].lev)){//左儿子大于右儿子
                    zig(p);//让左儿子“当爹”
                    erase(pool[p].rs,x);//当前节点转到了右儿子上，继续“追杀”
                }else{//同理
                    zag(p);
                    erase(pool[p].ls,x);
                }
            }
        }
    }else if(x<pool[p].val){//递归
        erase(pool[p].ls,x);
        push_up(p);
        if(pool[p].ls&&pool[pool[p].ls].lev>pool[p].lev)zig(p);
    }else{//x>pool[p].val
        erase(pool[p].rs,x);
        push_up(p);
        if(pool[p].rs&&pool[pool[p].rs].lev>pool[p].lev)zag(p);
    }
}

1.4. 其他查找操作

Treap 的查找操作跟普通的二叉搜索树相同，这里不再赘述，直接放代码：

int rank(int p,int x){//查询比x小的数的个数+1
    if(p==nul){
        return 1;
    }else if(x==pool[p].val){
        return pool[pool[p].ls].siz+1;
    }else if(x<pool[p].val){
        return rank(pool[p].ls,x);
    }else{
        return pool[pool[p].ls].siz+pool[p].cnt+rank(pool[p].rs,x);
    }
}
int kth(int p,int x){//查询第x小的树
    if(p==nul){
        return INF;
    }else if(pool[pool[p].ls].siz>=x){
        return kth(pool[p].ls,x);
    }else if(pool[pool[p].ls].siz+pool[p].cnt>=x){
        return pool[p].val;
    }else{
        return kth(pool[p].rs,x-pool[pool[p].ls].siz-pool[p].cnt);
    }
}
int count(int p,int x){//查询x有多少个
    if(p==nul){
        return 0;
    }else if(x==pool[p].val){
        return pool[p].cnt;
    }else if(x<pool[p].val){
        return count(pool[p].ls,x);
    }else{
        return count(pool[p].rs,x);
    }
}

2. Treap 的应用

Treap 可以维护很多信息，还可以扩展到树套树、可持久化等神奇科技。总之，Treap 十分实用。

3. 坑点与吐槽

1. Treap 的旋转操作十分毒瘤，如果在考场上忘了怎么写可以把这张图画一画。
2. 一定要考虑边界情况！一定要考虑边界情况！一定要考虑边界情况！
3. 一定要随手push_up！
4. Treap 的模板题博主调了甚至几个月才调出来（我太菜了QAQ）。如图：我真有毅力（小声

4. 完整代码

最后，附赠一份能通过模板题洛谷P3369的代码：

#include <iostream>
#include <queue>
using namespace std;
#define MAXN 100000
#define INF 0x3fffffff
struct treap_node{
    int ls,rs;
    int val;
    int cnt,siz,lev;
};
treap_node pool[MAXN+5];
int treap_tail;
const int nul=0;
queue<int> treap_rubbish;
int new_treap_node(){
    int res=0;
    if(treap_rubbish.empty()){
        res=++treap_tail;
    }else{
        res=treap_rubbish.front();
        treap_rubbish.pop();
    }
    pool[res].cnt=pool[res].siz=pool[res].ls=pool[res].rs=0;
    pool[res].val=0;
    pool[res].lev=rand();
    return res;
}
void delete_treap_node(int &p){
    treap_rubbish.push(p);
    p=0;
}
struct treap{
    int root;
    treap(){
        root=nul;
    }
    void zig(int &p){
        int tmp=pool[p].ls;
        pool[p].ls=pool[tmp].rs;
        pool[tmp].rs=p;
        push_up(p);push_up(tmp);
        p=tmp;
    }
    void zag(int &p){
        int tmp=pool[p].rs;
        pool[p].rs=pool[tmp].ls;
        pool[tmp].ls=p;
        push_up(p);push_up(tmp);
        p=tmp;
    }
    void push_up(int p){
        pool[p].siz=pool[pool[p].ls].siz+pool[pool[p].rs].siz+pool[p].cnt;
    }
    void insert(int &p,int x){
        if(p==nul){
            p=new_treap_node();
            pool[p].val=x;
            pool[p].siz=pool[p].cnt=1;
        }else if(x==pool[p].val){
            pool[p].cnt++;
            push_up(p);
        }else if(x<pool[p].val){
            insert(pool[p].ls,x);
            push_up(p);
            if(pool[pool[p].ls].lev>pool[p].lev)zig(p);
        }else{//x>pool[p].val
            insert(pool[p].rs,x);
            push_up(p);
            if(pool[pool[p].rs].lev>pool[p].lev)zag(p);
        }
    }
    void erase(int &p,int x){
        if(p==nul){
        }else if(x==pool[p].val){
            if(pool[p].cnt>1){
                pool[p].cnt--;push_up(p);
            }else{
                pool[p].cnt=0;
                if(!(pool[p].ls||pool[p].rs)){
                    delete_treap_node(p);
                }else{
                    if(pool[p].rs==0||
                    (pool[p].ls&&pool[pool[p].ls].lev>pool[pool[p].rs].lev)){
                        zig(p);
                        erase(pool[p].rs,x);
                    }else{
                        zag(p);
                        erase(pool[p].ls,x);
                    }
                }
            }
        }else if(x<pool[p].val){
            erase(pool[p].ls,x);
            push_up(p);
            if(pool[p].ls&&pool[pool[p].ls].lev>pool[p].lev)zig(p);
        }else{//x>pool[p].val
            erase(pool[p].rs,x);
            push_up(p);
            if(pool[p].rs&&pool[pool[p].rs].lev>pool[p].lev)zag(p);
        }
    }
    int rank(int p,int x){
        if(p==nul){
            return 1;
        }else if(x==pool[p].val){
            return pool[pool[p].ls].siz+1;
        }else if(x<pool[p].val){
            return rank(pool[p].ls,x);
        }else{
            return pool[pool[p].ls].siz+pool[p].cnt+rank(pool[p].rs,x);
        }
    }
    int kth(int p,int x){
        if(p==nul){
            return INF;
        }else if(pool[pool[p].ls].siz>=x){
            return kth(pool[p].ls,x);
        }else if(pool[pool[p].ls].siz+pool[p].cnt>=x){
            return pool[p].val;
        }else{
            return kth(pool[p].rs,x-pool[pool[p].ls].siz-pool[p].cnt);
        }
    }
    int count(int p,int x){
        if(p==nul){
            return 0;
        }else if(x==pool[p].val){
            return pool[p].cnt;
        }else if(x<pool[p].val){
            return count(pool[p].ls,x);
        }else{
            return count(pool[p].rs,x);
        }
    }
};
int main(){
    srand(19260817);
    treap a;
    int n;cin>>n;
    while(n--){
        int op,x;cin>>op>>x;
        if(op==1){
            a.insert(a.root,x);
        }else if(op==2){
            a.erase(a.root,x);
        }else if(op==3){
            cout<<a.rank(a.root,x)<<endl;
        }else if(op==4){
            cout<<a.kth(a.root,x)<<endl;
        }else if(op==5){
            cout<<a.kth(a.root,a.rank(a.root,x)-1)<<endl;
        }else if(op==6){
            cout<<a.kth(a.root,a.rank(a.root,x)+a.count(a.root,x))<<endl;
        }
    }
    return 0;
}

5.点一个赞！