Codeforces 521E - Cycling City（点双连通分量+分类讨论）

Codeforces 题面传送门 & 洛谷题面传送门

大家都是暴力找生成树然后跳路径，代码不到 50 行（暴论）的一说……好，那本蒟蒻决定提供一种代码 150 行，但复杂度也是线性的分类讨论做法。

首先大家都是从“如果存在两个环相交，就一定存在符合要求的路径”这个性质入手的，而我不是。注意到题目条件涉及“简单路径”，因此我首先想到的是，如果两个点 \(u,v\) 之间存在三条互不相交的路径，那么 \(u,v\) 在同一个点双连通分量中必定是必要条件，因此不同点双之间的点必然是没有贡献的，我们只用考虑同一点双中的点即可。

考虑什么样的点双中存在符合条件的两个点，通过手玩数据我发现，一个环的情况显然是不行的，其余情况都存在符合要求的两个点。因此直觉告诉我，一个点双中存在符合条件的两个点的充要条件就是这个点双不是一个环。事实也的确如此，考虑怎么构造符合条件的路径。

我们考虑随便定一个根节点，并以从根节点开始 DFS 找出点双的一棵 DFS 树，那么由于原图是一个点双，必然有与根节点 \(r\) 相连的树边只有一条，因为根据 DFS 树的性质，该点双中所有非树边都是连接 DFS 树上某个点与其祖先的边，因此如果根节点存在多个分叉，那么这些分叉代表的子树之间两两是没有边的，换句话说，去掉根节点后图不连通，不符合点双的定义。考虑就此分三种情况讨论：

1. 存在两个及以上与根节点相连的非树边

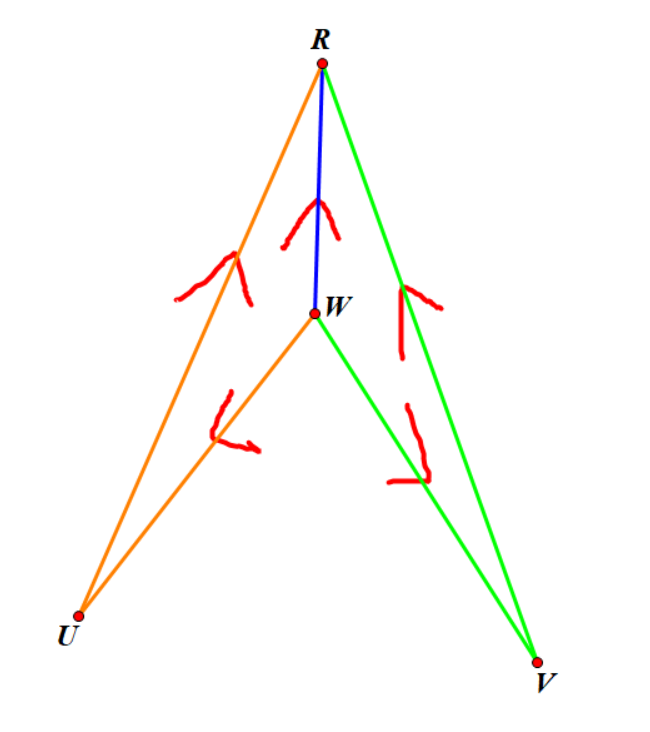
   假设这两条非树边分别是 \(r\to u\) 和 \(r\to v\)，那么考虑找出 \(w=\text{LCA}(u,v)\)，那么 \(r,w\) 之间存在三条符合要求的路径，一条是 \(w\) 直接跳到 \(r\)，一条是 \(w\) 向下走到 \(u\)，\(u\) 再到 \(r\)，一条是 \(w\) 向下走到 \(v\)，\(v\) 再到 \(r\)​​。

   如下图所示，三种颜色分别代表了三条不同的路径：

   

2. 只有一条与根节点相连的非树边

   显然，由于原图是一个点双，不能不存在非树边与根节点相连，否则去掉根节点唯一的儿子后，图就不连通了（这里假定点双大小 \(\ge 3\)，如果点双大小 \(\le 2\) 直接判掉即可）

   那么我们不妨假设这条非树边为 \(r\to u\)，到这里我们继续分类讨论：

   1. 如果 \(u\) 不是叶子

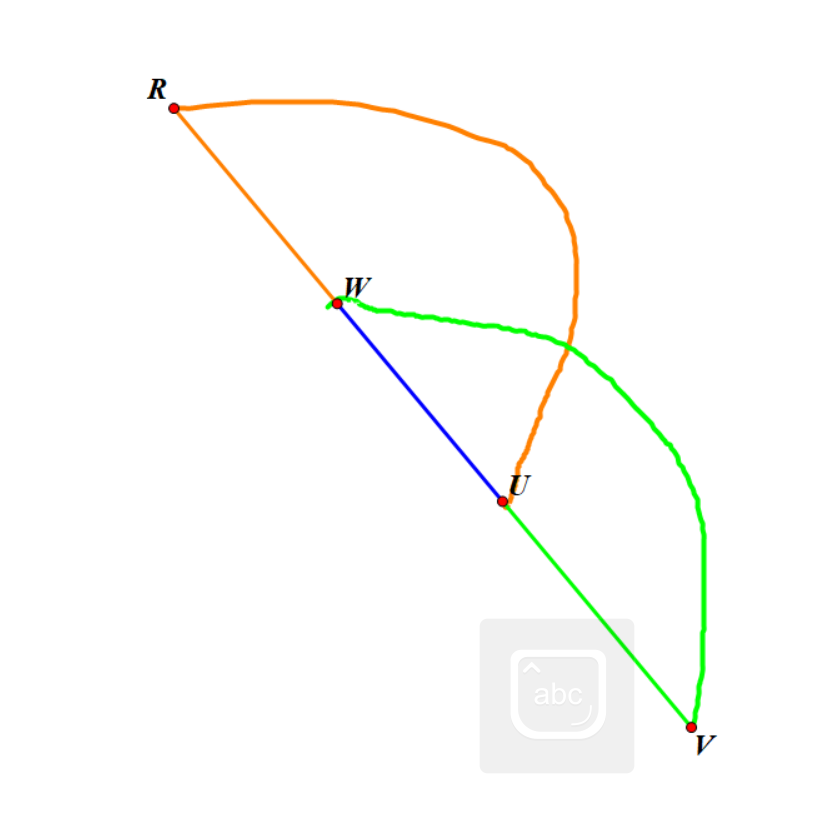
      那么我们考虑找到 \(u\) 子树中一个叶子 \(v\)，再找到所有与 \(v\) 相连的点中，深度最浅的那个点 \(w\)，还是根据图是一个点双这个性质，必然有 \(w\) 的深度严格浅于 \(u\) 的深度，否则去掉 \(w\) 之后图不连通，这样考虑 \(u\to w\) 的路径，有以下三条：

      • \(u\) 向上直接跳到 \(w\)
      • \(u\) 跳到根节点 \(r\)，再向下走到 \(w\)
      • \(u\) 向下走到 \(v\)，再向上跳到 \(w\)​

      

   2. 如果 \(u\) 是叶子

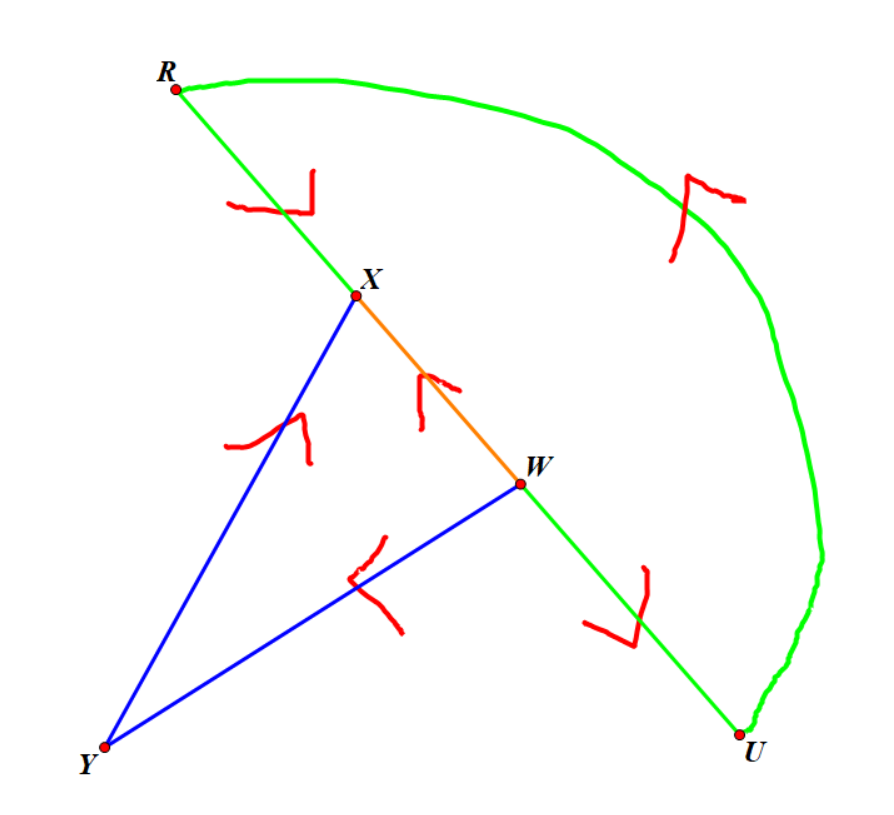
      我们考虑找到一条非树边，不同于 \(r\to u\) 这条边，并且这两条边至少有一个端点在 \(u\to r\) 这条链上，可以说明我们总能找到这样的边，否则图不满足点双的性质，读者自证不难，那么我们假设这条边为 \(x,y\)，其中 \(x\) 为深度较小者，设离 \(y\) 最近的、在 \(u\to r\) 这条链上的节点为 \(w\)，那么考虑构造这样三条 \(w\to x\) 的路径：

      • \(w\) 直接向上跳到 \(x\)
      • \(w\) 向下走到 \(y\)，再走到 \(x\)
      • \(w\) 向下走到 \(u\)，跳到 \(r\)，再向下走到 \(x\)​

      

分类讨论一下即可，复杂度 \(\mathcal O(n)\)

const int MAXN=2e5;
int n,m,U[MAXN+5],V[MAXN+5];
struct graph{
	int hd[MAXN+5],to[MAXN*2+5],nxt[MAXN*2+5],ec=1;
	void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
} g,ng,t;
int dfn[MAXN+5],low[MAXN+5],tim=0;
int stk[MAXN+5],tp=0,bel[MAXN+5],cmp=0,in_stk[MAXN+5];
void tarjan(int x){
//	printf("tarjan %d\n",x);
	dfn[x]=low[x]=++tim;
	for(int e=g.hd[x];e;e=g.nxt[e]){
		int y=g.to[e];
		if(!dfn[y]){
			stk[++tp]=e>>1;in_stk[e>>1]=1;
			tarjan(y);chkmin(low[x],low[y]);
			if(low[y]>=dfn[x]){
//				printf("find an edcc %d %d\n",x,y);
				cmp++;int o;do{
					o=stk[tp--];bel[o]=cmp;
					in_stk[o]=0;
				} while(o^(e>>1));
			}
		} else {
			chkmin(low[x],dfn[y]);
			if(dfn[y]<dfn[x]&&!in_stk[e>>1]){
				stk[++tp]=e>>1;in_stk[e>>1]=1;
			}
		}
	}
}
vector<int> bp[MAXN+5];
int in[MAXN+5],fa[MAXN+5],dep[MAXN+5],deg[MAXN+5];
bool vis[MAXN+5],ont[MAXN+5];
void dfs(int x){
	vis[x]=1;
	for(int e=ng.hd[x];e;e=ng.nxt[e]){
		int y=ng.to[e];
		if(!vis[y]){
			ont[e>>1]=1;t.adde(x,y);
			fa[y]=x;deg[x]++;deg[y]++;dep[y]=dep[x]+1;dfs(y);
		}
	}
}
void prt(vector<int> res1,vector<int> res2,vector<int> res3){
	puts("YES");
	printf("%d",res1.size());for(int x:res1) printf(" %d",x);printf("\n");
	printf("%d",res2.size());for(int x:res2) printf(" %d",x);printf("\n");
	printf("%d",res3.size());for(int x:res3) printf(" %d",x);printf("\n");
	exit(0);
}
void work(int id){
	for(int e:bp[id]) ng.adde(U[e],V[e]),ng.adde(V[e],U[e]);
	dfs(U[bp[id][0]]);int rt=U[bp[id][0]],cnt=0;
	for(int e=ng.hd[rt];e;e=ng.nxt[e]) cnt+=(!ont[e>>1]);
	assert(cnt>=1);
	if(cnt>=2){
		int x=0,y=0;vector<int> p1,p2,p3;p1.pb(rt),p2.pb(rt);
		for(int e=ng.hd[rt];e;e=ng.nxt[e]) if(!ont[e>>1]){
			if(!x) x=ng.to[e];else if(!y) y=ng.to[e];
		} if(dep[x]<dep[y]) swap(x,y);
		while(dep[x]>dep[y]) p1.pb(x),x=fa[x];
		while(x^y) p1.pb(x),p2.pb(y),x=fa[x],y=fa[y];
		p1.pb(x);p2.pb(x);
		while(x^rt) p3.pb(x),x=fa[x];p3.pb(rt);
		reverse(p3.begin(),p3.end());prt(p1,p2,p3);
	} else {
		int p=0,pe=0;
		for(int e=ng.hd[rt];e;e=ng.nxt[e]) if(!ont[e>>1])
			p=ng.to[e],pe=e>>1;
		if(deg[p]!=1){
			int q=p;while(deg[q]!=1){
				for(int e=t.hd[q];e;e=t.nxt[e])
					if(t.to[e]!=fa[q]){q=t.to[e];break;}
			} int r=0;for(int e=ng.hd[q];e;e=ng.nxt[e])
				if(!r||dep[r]>dep[ng.to[e]]) r=ng.to[e];
			vector<int> p1,p2,p3;int cp=p,cq=q;
			while(cp^r) p1.pb(cp),cp=fa[cp];p1.pb(cp);
			while(cp^rt) p2.pb(cp),cp=fa[cp];p2.pb(rt);
			reverse(p2.begin(),p2.end());p2.insert(p2.begin(),p);
			while(cq^p) p3.pb(cq),cq=fa[cq];p3.pb(cq);
			reverse(p3.begin(),p3.end());p3.pb(r);
			prt(p1,p2,p3);
		} else {
			int cp=p;static bool on_ch[MAXN+5]={0};
			while(cp^rt) on_ch[cp]=1,cp=fa[cp];on_ch[rt]=1;
			int u=0,v=0;vector<int> p1,p2,p3;
			for(int e=1;e<=(ng.ec>>1);e++) if(!ont[e]&&e!=pe){
				int x=ng.to[e<<1],y=ng.to[e<<1|1];
				if(on_ch[x]||on_ch[y]){u=x;v=y;break;}
			} if(dep[u]<dep[v]) swap(u,v);
			while(!on_ch[u]) p1.pb(u),u=fa[u];p1.pb(u);
			reverse(p1.begin(),p1.end());p1.pb(v);
			int cu=u,cv=v;while(cu^v) p2.pb(cu),cu=fa[cu];p2.pb(v);
			cu=p;while(cv^rt) p3.pb(cv),cv=fa[cv];p3.pb(rt);
			while(cu^u) p3.pb(cu),cu=fa[cu];p3.pb(cu);
			reverse(p3.begin(),p3.end());prt(p1,p2,p3);
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&U[i],&V[i]);
		g.adde(U[i],V[i]);g.adde(V[i],U[i]);
	} for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
	for(int i=1;i<=m;i++) bp[bel[i]].pb(i);
//	for(int i=1;i<=m;i++) printf("%d\n",bel[i]);
	for(int id=1;id<=cmp;id++){
		int cc=0;
		for(int e:bp[id]){
			if(!in[U[e]]) in[U[e]]=1,cc++;
			if(!in[V[e]]) in[V[e]]=1,cc++;
		} if(cc<bp[id].size()){
			work(id);
		} for(int e:bp[id]) in[U[e]]=in[V[e]]=0;
	} puts("NO");
	return 0;
}