C#实现RSA加密与解密、签名与认证（转）

一、RSA简介

RSA公钥加密算法是1977年由Ron Rivest、Adi Shamirh和LenAdleman在（美国麻省理工学院）开发的。RSA取名来自开发他们三者的名字。RSA是目前最有影响力的公钥加密算法，它能够抵抗到目前为止已知的所有密码攻击，已被ISO推荐为公钥数据加密标准。RSA算法基于一个十分简单的数论事实：将两个大素数相乘十分容易，但那时想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和操作。
RSA是被研究得最广泛的公钥算法，从提出到现在已近二十年，经历了各种攻击的考验，逐渐为人们接受，普遍认为是目前最优秀的公钥方案之一。RSA的安全性依赖于大数的因子分解，但并没有从理论上证明破译RSA的难度与大数分解难度等价。即RSA的重大缺陷是无法从理论上把握它的保密性能如何，而且密码学界多数人士倾向于因子分解不是NPC问题。
RSA的缺点主要有：
A)产生密钥很麻烦，受到素数产生技术的限制，因而难以做到一次一密。

B)分组长度太大，为保证安全性，n 至少也要 600bits以上，使运算代价很高，尤其是速度较慢，较对称密码算法慢几个数量级；且随着大数分解技术的发展，这个长度还在增加，不利于数据格式的标准化。目前，SET(Secure Electronic Transaction)协议中要求CA采用2048bits长的密钥，其他实体使用1024比特的密钥。

C)RSA密钥长度随着保密级别提高，增加很快。下表列出了对同一安全级别所对应的密钥长度。

这种算法1978年就出现了，它是第一个既能用于数据加密也能用于数字签名的算法。它易于理解和操作，也很流行。算法的名字以发明者的名字命名：Ron Rivest, 
AdiShamir 和Leonard Adleman。早在1973年，英国国家通信总局的数学家Clifford Cocks就发现了类似的算法。但是他的发现被列为绝密，直到1998年才公诸于世。
RSA算法是一种非对称密码算法，所谓非对称，就是指该算法需要一对密钥，使用其中一个加密，则需要用另一个才能解密。
RSA的算法涉及三个参数，n、e1、e2。
其中，n是两个大质数p、q的积，n的二进制表示时所占用的位数，就是所谓的密钥长度。
e1和e2是一对相关的值，e1可以任意取，但要求e1与(p-1)*(q-1)互质；再选择e2，要求(e2*e1)mod((p-1)*(q-1))=1。
(n及e1),(n及e2)就是密钥对。
RSA加解密的算法完全相同,设A为明文，B为密文，则：A=B^e1 mod n；B=A^e2 mod n；
e1和e2可以互换使用，即：

A=B^e2 mod n；B=A^e1 mod n;

二、MD5加密介绍

参考：http://blog.csdn.net/wonsoft/article/details/5913572
MD5的全称是message-digest algorithm 5(信息-摘要算法，在90年代初由mit laboratory for computer science和rsa data security inc的ronald l. rivest开发出来， 经md2、md3和md4发展而来。
MD5具有很好的安全性(因为它具有不可逆的特征,加过密的密文经过解密后和加密前的东东相同的可能性极小)

1.  
   public string GetStrMd5(string ConvertString)
2.  
   {
3.  
   string strBodyBase64 = Convert.ToBase64String(Encoding.UTF8.GetBytes(ConvertString));
4.  
   string t2=System.Web.Security.FormsAuthentication.HashPasswordForStoringInConfigFile(strBodyBase64, "MD5").ToUpper();
5.  
   return t2;
6.  
   }

三、C#对PKCS＃8编码的RSA私钥进行签名

 对MD5加密后的长度为32的密文进行PKCS8的RSA签名的方法：

1.  

四、C#实现RSA加密与解密、签名与认证常用方法

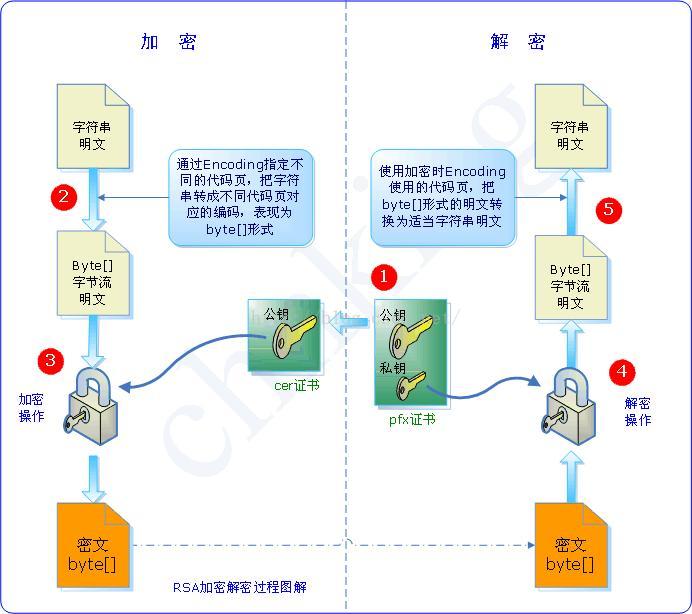
1.RSA加密解密：
　(1)获取密钥，这里是产生密钥，实际应用中可以从各种存储介质上读取密钥 (2)加密 (3)解密
2.RSA签名和验证
　(1)获取密钥，这里是产生密钥，实际应用中可以从各种存储介质上读取密钥 (2)获取待签名的Hash码 (3)获取签名的字符串 (4)验证
3.公钥与私钥的理解：
　(1)私钥用来进行解密和签名，是给自己用的。
　(2)公钥由本人公开，用于加密和验证签名，是给别人用的。
    (3)当该用户发送文件时，用私钥签名，别人用他给的公钥验证签名，可以保证该信息是由他发送的。当该用户接受文件时，别人用他的公钥加密，他用私钥解密，可以保证该信息只能由他接收到

源地址：https://blog.csdn.net/u010678947/article/details/48652875