tarjan求双联通分量（割点，割边）

之前一直对tarjan算法的这几种不同应用比较混淆...我太弱啦！

被BLO暴虐滚过来

用tarjan求点双，很多神犇都给出了比较详细的解释和证明，在这里就不讲了（其实是这只蒟蒻根本不会orz）

这里放一下定义

这篇博客主要讲一讲求割点，点双的板子实现以及详细解释

先yy这样一道题：

有n个点，m条边，保证给出的是一个联通图，求割点

（真·最裸割点）

这道题就可以用下面这份代码实现

#pragma GCC optimize("O2")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<limits.h>
#include<ctime>
#define N 100001
typedef long long ll;
const int inf=0x3fffffff;
const int maxn=2017;
using namespace std;
inline int read()
{
    int f=1,x=0;char ch=getchar();
    while(ch>'9'|ch<'0')
    {
        if(ch=='-')
        f=-1;
        ch=getchar();
    }
    while(ch<='9'&&ch>='0')
    {
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }
    return f*x;
}
struct tsdl{
	int to,w,next ;
} edge[N*4];
int tot,head[N],dfn[N],low[N],fa[N],son[N],size[N];
bool iscut[N];
void add(int ui,int vi)
{
	edge[++tot].next=head[ui];
	edge[tot].to=vi;
	head[ui]=tot;
}
void tarjan(int x)
{
	dfn[x]=low[x]=++tot;
	size[x]=1;
	for(int i=head[x];i!=-1;i=edge[i].next)
	{
		int v=edge[i].to;
		if(v==fa[x])continue;
		if(!dfn[v])
		{
			son[x]++;//x的子树++
			fa[v]=x;//v的父亲是x
			tarjan(v);
			size[x]+=size[v];//x所连节点的个数
			low[x]=min(low[x],low[v]);
			if(dfn[x]<=low[v])
			{
				iscut[x]=1;//找到割点
			}
		}
		else low[x]=min(low[x],dfn[v]);
	}
	if(fa[x]==0&&son[x]<=1)
	iscut[x]=0;//根节点，特判处理
}
int main()
{
	memset(head,-1,sizeof(head));
	int n=read(),m=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read();
		add(u,v);
		add(v,u);
	}
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i])tarjan(i);
	}
	for(int i=1;i<=n;i++)
	if(iscut[i])cout<<i<<endl;
}

例如我们输入

5 5
1 2
2 3
1 3
3 4
4 5

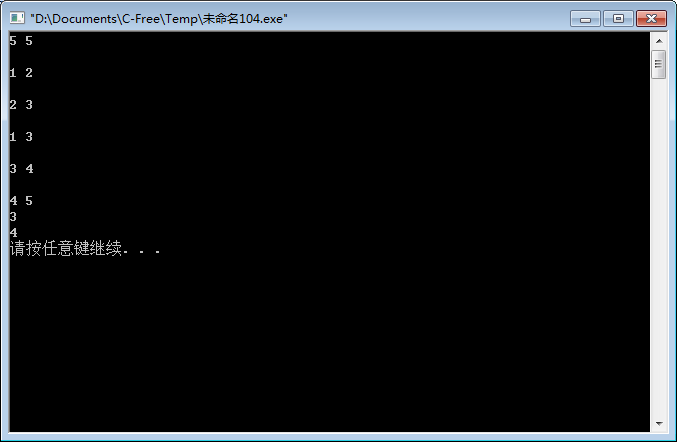
程序完美の输出了 3,4

是不是很棒啊x

那么我们要统计点双的数量要怎么处理呢？

显然能发现，我们求出一个割点之后，被割点分成的几部分都能分别与这个割点组成一个点双

那么我们只需要统计每个割点被访问次数即可

更改之后的代码：

#pragma GCC optimize("O2")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<limits.h>
#include<ctime>
#define N 100001
typedef long long ll;
const int inf=0x3fffffff;
const int maxn=2017;
using namespace std;
inline int read()
{
    int f=1,x=0;char ch=getchar();
    while(ch>'9'|ch<'0')
    {
        if(ch=='-')
        f=-1;
        ch=getchar();
    }
    while(ch<='9'&&ch>='0')
    {
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }
    return f*x;
}
struct tsdl{
	int to,w,next ;
} edge[N*4];
int tot,head[N],dfn[N],low[N],fa[N],son[N],size[N];
bool iscut[N];
void add(int ui,int vi)
{
	edge[++tot].next=head[ui];
	edge[tot].to=vi;
	head[ui]=tot;
}
int ans;
void tarjan(int x)
{
	if(iscut[x])ans++;//统计x1
	dfn[x]=low[x]=++tot;
	size[x]=1;
	int tmp=0;
	for(int i=head[x];i!=-1;i=edge[i].next)
	{
		int v=edge[i].to;
		if(edge[i].to==fa[x])continue;
		if(!dfn[v])
		{
			son[x]++;
			fa[v]=x;
			tarjan(v);
			size[x]+=size[v];
			low[x]=min(low[x],low[v]);
			if(dfn[x]<=low[v])
			{
				iscut[x]=1;//找到割点
				ans++;//统计x2
			}
		}
		else low[x]=min(low[x],dfn[v]);
	}
	if(fa[x]==0&&son[x]<=1)
	iscut[x]=0;//根节点，特判处理
}
int main()
{
	memset(head,-1,sizeof(head));
	int n=read(),m=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read();
		add(u,v);
		add(v,u);
	}
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i])tarjan(i);
	}
	for(int i=1;i<=n;i++)
	if(iscut[i])cout<<i<<endl;
	cout<<ans;
}

输出就是直接

当然对他做一点小小的改动也可以实现求桥..

只需要对于每次记录iscut  改为记录二维数组cutedge[x][v]即可

需要注意的是 这里的条件不同于求割点的小于等于 这里需要low[v]严格大于dfn[x]