POJ-3436 ACM Computer Factory 最大流 为何拆点

题目链接：https://cn.vjudge.net/problem/POJ-3436

题意

懒得翻，找了个题意。

流水线上有N台机器装电脑，电脑有P个部件，每台机器有三个参数，产量，输入规格，输出规格;输入规格中0表示改部件不能有，1表示必须有，2无所谓;输出规格中0表示改部件没有，1表示有。问如何安排流水线（如何建边）使产量最高。

思路

建图如下



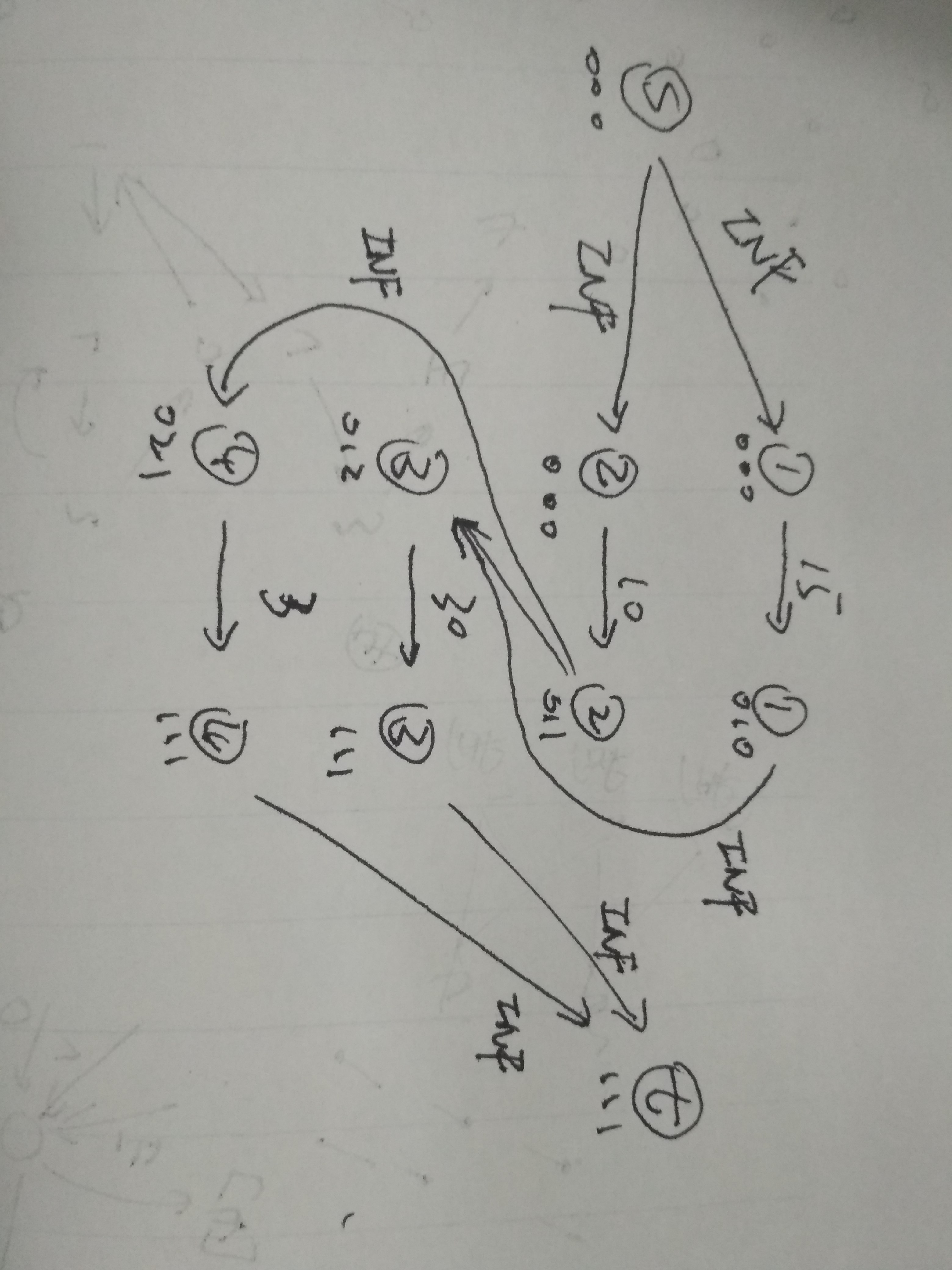
说一下为什么要拆点，若不拆点：

当每台机器节点的入度大于1且出度大于1时，经过这个节点的流量没法限制在容量下。

提交过程

AC

代码

#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=50+20, INF=1e8;
struct Edge{
    int from,to,cap,flow;
    Edge(int u,int v,int c,int f):
        from(u), to(v), cap(c), flow(f) {}
};
struct Dinic{
    int n, m, s, t;
    vector<int> G[maxn];
    vector<Edge> edges;
    bool vis[maxn];
    int dep[maxn], cur[maxn];
    void init(int n){
        this->n=n;
        for (int i=0;i<=n;i++) G[i].clear();
        edges.clear();
    }
    void addEdge(int from, int to, int cap){
        edges.push_back(Edge(from, to, cap, 0));
        edges.push_back(Edge(to, from, 0, 0));
        m=edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }
    bool bfs(void){
        memset(vis, false, sizeof(vis));
        queue<int> Q;
        vis[s]=true;
        dep[s]=0;

        Q.push(s);
        while(!Q.empty()){
            int x=Q.front(); Q.pop();
            for(int i=0;i<G[x].size();i++){
                Edge &e=edges[G[x][i]];
                if(!vis[e.to] && e.cap>e.flow){
                    vis[e.to]=1;
                    dep[e.to]=dep[x]+1;
                    Q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int dfs(int x, int a){//a当前为止所有弧的最小残量
        if(x==t || a==0)return a;
        int flow=0, f;
        for(int &i=cur[x];i<G[x].size();i++) {//cur当前弧优化
            Edge &e=edges[G[x][i]];
            if(dep[e.to]==dep[x]+1 && (f=dfs(e.to, min(a, e.cap-e.flow)))>0){
                e.flow+=f;
                edges[G[x][i]^1].flow-=f;
                flow+=f;
                a-=f;
                if(a==0)break;
            }
        }
        return flow;
    }
    int maxFlow(int s, int t){
        this->s=s; this->t=t;

        int flow=0;
        while(bfs()){
            memset(cur, 0, sizeof(cur));
            flow+=dfs(s, INF);
        }
        return flow;
    }
    void bugs(void){
        for (int i=0; i<=n; i++){
            printf("%d: ", i);
            for (int j=0; j<G[i].size(); j++)
                if (edges[G[i][j]].cap!=0)
                    printf("%d(%d) ", edges[G[i][j]].to, edges[G[i][j]].cap);
            printf("\n");
        }
    }

    void show(int st, int end){
        int from[maxn*maxn], to[maxn*maxn], flow[maxn*maxn];
        int size=0;
        int ans=maxFlow(0, 1);

        if (ans==0){
            printf("0 0\n");
            return;
        }

        for (int i=st; i<=end; i++){
            for (int j=0; j<G[i].size(); j++){
                Edge &e=edges[G[i][j]];
                if (e.cap==INF && e.flow>0 && e.from!=0 && e.to!=1){
                    from[size]=e.from;
                    to[size]=e.to;
                    flow[size++]=e.flow;
                }
            }
        }

        printf("%d %d\n", ans, size);
        for (int i=0; i<size; i++)
            printf("%d %d %d\n", from[i]/2, to[i]/2, flow[i]);
    }
}dinic;

int n, m, in[maxn][15], out[maxn][15], cap[maxn];
bool match(int j, int i){
    for (int k=0; k<m; k++)
        if (out[j][k]!=in[i][k] && in[i][k]!=2)
            return false;
    return true;
}

void makeGraph(void){
    for (int i=2; i<=n+1; i++){
        dinic.addEdge(i*2-2, i*2-1, cap[i]);
        for (int j=2; j<=n+1; j++) if (i!=j){
            if (match(j, i)) dinic.addEdge(j*2-1, i*2-2, INF);
        }
        if (match(0, i)) dinic.addEdge(0, i*2-2, INF);
        if (match(i, 1)) dinic.addEdge(i*2-1, 1, INF);
    }
}

int main(void){
    int from, to, tmp;
    while (scanf("%d%d", &m, &n)==2 && n){
        dinic.init(n*2+1);

        for (int i=0; i<m; i++) in[1][i]=1;
        for (int i=0; i<m; i++) out[0][i]=0;
        for (int i=2; i<=n+1; i++){
            scanf("%d", &cap[i]);
            for (int j=0; j<m; j++) scanf("%d", &in[i][j]);
            for (int j=0; j<m; j++) scanf("%d", &out[i][j]);
        }

        makeGraph();
        // dinic.bugs();
        dinic.show(2, n*2+1);
    }

    return 0;
}

Time	Memory	Length	Lang	Submitted
208kB	3993	C++	2018-08-17 04:42:53