仙人掌的同构(hash)

关于仙人掌的同构，主要是我太蒟蒻了QAQ，问了好几位大佬才弄好。

手撕仙人掌，你得先有手套 ，你得先了解以下基本知识

a.点双连通分量，没什么好说得，仙人掌上有环，判环用点双

b.树的hash点这里

c.仙人掌点这里　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

对于一棵仙人掌，我们通过一些方法来简化:　　　　　　　　　　　　　　　　　

我们最讨厌的是环，假如说没有环，那么树的hash还是蛮简单的。　　　　　　　　　　

OK那么就是圆方树了，如果你还不知道什么是圆方树，请自行百度或者点这里。

当然对于判定仙人掌的同构，不需要一颗完整的圆方树，只需要在环中间建点

单纯地表示一个环，使用最小表示法（这部分内容我稍后补充QAQ）

单纯地表示一棵树，hash。

嗯，如果你觉得我上面说得十分模糊，那么是正确的，因为还没有开始呢　　^_^

（我其实是不会告诉你我没有用tarjan和完整的圆方树的）

e.g.一个只有一个环的仙人掌

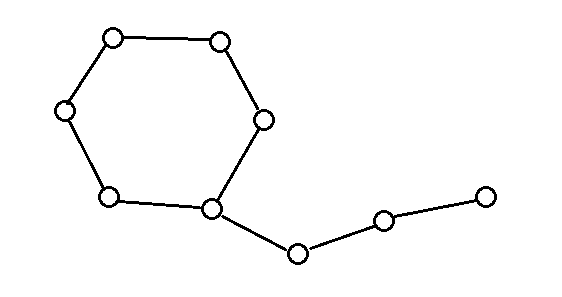
假设我们是这样搜索的

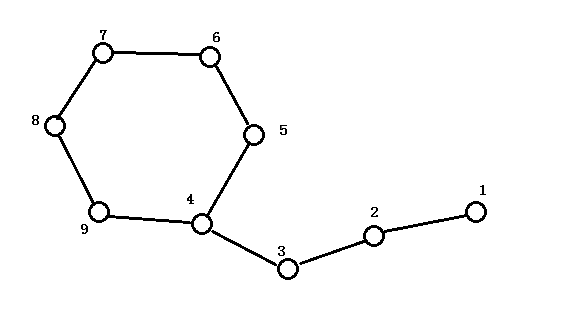
那么在dfs的过程中，要判定一个点在不在环上，记录它的父节点这样在回溯到4时，发现他有一个不是自己儿子的子节点（9）

哈，那就是环的另一端了。

这时抓出9，一直回溯父亲直到4被枚举到，整个环就被揪了出来。

新建一个节点，（在圆方树里则称方点）依次连边。

而对于非环上边直接连就好了

像这样就建立了一个独立出原图的树（一位大佬是这样描述的）

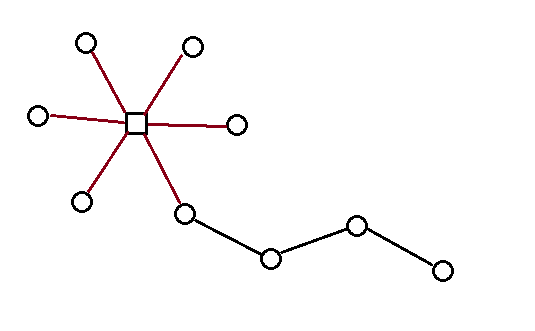
多么优雅的一棵树

好了，现在它是无根的找一下树的重心

新建一个根节点hash一下就好了^_^

你真的觉得这就完了

你太天真了

环是不能这样子搞的

正确打开方式：

别忘了真正的环上点是有顺序的

假如说这个环的方点（中间那个新建点）是根，跑最小表示法（然而我代码里没有这一项QAQ我改天加上）

对于一个普通树节点比如说这样

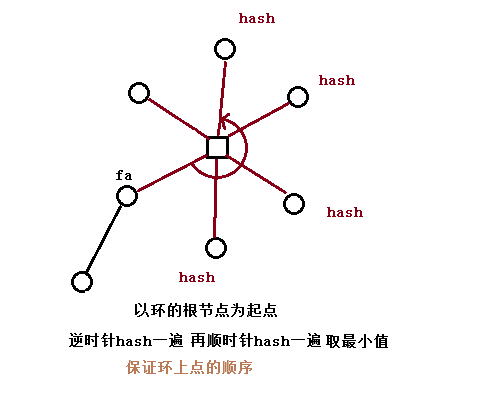
这样就可以了

代码实现

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 typedef unsigned long long ult;
 const ult seed1=1324983271ull;
 const ult seed2=4327894239ull;
 const ult lth1=9301248721ull;
 const ult lth2=8317498371ull;
 int nt,mt;
 bool cmp(ult x,ult y)
 {
     return x<y;
 }
 struct pnt{
     int hd;
     int sh;
     int fa;
     int wgt;
     bool ong;
     bool vis;
     bool chkd;
     ult has;
 };
 struct ent{
     int twd;
     int lst;
 };
 struct Cactus{
     pnt p[];
     ent e[];
     ent r[];
     ult st[];
     int rt[];
     int n,m;
     int sqn;
     int cnt;
     int cmt;
     void e_ade(int f,int t)
     {
         cnt++;
         e[cnt].twd=t;
         e[cnt].lst=p[f].hd;
         p[f].hd=cnt;
     }
     void r_ade(int f,int t)
     {
         cmt++;
         r[cmt].twd=t;
         r[cmt].lst=p[f].sh;
         p[f].sh=cmt;
     }
     void tr_dfs(int x,int f)
     {
         p[x].vis=true;
         for(int i=p[x].hd;i;i=e[i].lst)
         {
             int to=e[i].twd;
             if((i^f)==)continue;
             if(!p[to].vis)
             {
                 p[to].fa=x;
                 p[x].ong=false;
                 tr_dfs(to,i);
                 if(!p[x].ong)
                 {
                     r_ade(x,to);
                     r_ade(to,x);
                 }
             }else{
                 if(p[to].chkd)continue;
                 sqn++;
                 int u=x;
                 for(u=x;;u=p[u].fa)
                 {
                     r_ade(n+sqn,u);
                     r_ade(u,n+sqn);
                     p[u].ong=true;
                     if(u==to)break;
                 }
             }
         }
         p[x].chkd=true;
     }
     void gravity(int x,int f)
     {
         p[x].wgt=;
         bool fl=true;
         for(int i=p[x].sh;i;i=r[i].lst)
         {
             int to=r[i].twd;
             if(to==f)continue;
             gravity(to,x);
             p[x].wgt+=p[to].wgt;
             if(p[to].wgt*>sqn+n)
                 fl=false;
         }
         if((sqn+n-p[x].wgt)*>sqn+n)
             fl=false;
         if(fl)
         {
             if(rt[])
             {
                 rt[]=x;
             }else{
                 rt[]=x;
             }
         }
     }
     void Hash(int x,int f)
     {
         int top=;
         for(int i=p[x].sh;i;i=r[i].lst)
         {
             int to=r[i].twd;
             if(to==f)continue;
             Hash(to,x);
         }
         if(x<=n)
         {
             for(int i=p[x].sh;i;i=r[i].lst)
             {
                 int to=r[i].twd;
                 if(to==f)continue;
                 st[++top]=p[to].has;
             }
             sort(st+,st+top+,cmp);
             p[x].has=seed1;
             for(int i=;i<=top;i++)
             {
                 p[x].has=((p[x].has*lth1+st[i])^st[i])+st[i];
             }
         }else{
             int i;
             for(i=p[x].sh;i;i=r[i].lst)
             {
                 if(r[i].twd==f)
                     break;
             }
             for(i=r[i].lst;i;i=r[i].lst)
             {
                 int to=r[i].twd;
                 st[++top]=p[to].has;
             }
             for(i=p[x].sh;i;i=r[i].lst)
             {
                 int to=r[i].twd;
                 if(to==f)
                     break;
                 st[++top]=p[to].has;
             }
             ult tmp1=seed2,tmp2=seed2;
             for(i=;i<=top;i++)
             {
                 tmp1=((tmp1*lth2+st[i])^st[i])+st[i];
             }
             for(i=top;i;i--)
             {
                 tmp2=((tmp2*lth2+st[i])^st[i])+st[i];
             }
             p[x].has=min(tmp1,tmp2);
             p[x].has*=lth2;
         }
     }
     ult solve(int nn,int mm)
     {
         n=nn;
         m=mm;
         cnt=;
         for(int i=;i<=m;i++)
         {
             int x;
             int y;
             scanf("%d%d",&x,&y);
             e_ade(x,y);
             e_ade(y,x);
         }
         tr_dfs(,);
         gravity(,);
         r_ade(,rt[]);
         if(rt[])
         {
             r_ade(,rt[]);
             for(int i=p[rt[]].sh;i;i=r[i].lst)
             {
                 if(r[i].twd==rt[])
                     r[i].twd=;
             }
             for(int i=p[rt[]].sh;i;i=r[i].lst)
             {
                 if(r[i].twd==rt[])
                     r[i].twd=;
             }
         }
         Hash(,);
         return p[].has;
     }
 }C[];
 int main()
 {
     scanf("%d%d",&nt,&mt);
     if(C[].solve(nt,mt)==C[].solve(nt,mt))
     {
         printf("YES\n");
     }else{
         printf("NO\n");
     }
     return ;
 }

大概就是这样了^_^