CF149D 区间dp

http://codeforces.com/problemset/problem/149/D

D. Coloring Brackets

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Once Petya read a problem about a bracket sequence. He gave it much thought but didn't find a solution. Today you will face it.

You are given string s. It represents a correct bracket sequence. A correct bracket sequence is the sequence of opening ("(")
and closing (")") brackets, such that it is possible to obtain a correct mathematical expression from it, inserting numbers and operators between
the brackets. For example, such sequences as "(())()" and "()"
are correct bracket sequences and such sequences as ")()" and "(()"
are not.

In a correct bracket sequence each bracket corresponds to the matching bracket (an opening bracket corresponds to the matching closing bracket and vice versa). For example, in a bracket sequence shown of the figure below, the third bracket corresponds to the
matching sixth one and the fifth bracket corresponds to the fourth one.

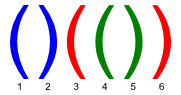
You are allowed to color some brackets in the bracket sequence so as all three conditions are fulfilled:

• Each bracket is either not colored any color, or is colored red, or is colored blue.
• For any pair of matching brackets exactly one of them is colored. In other words, for any bracket the following is true: either it or the matching bracket that corresponds to it is colored.
• No two neighboring colored brackets have the same color.

Find the number of different ways to color the bracket sequence. The ways should meet the above-given conditions. Two ways of coloring are considered different if they differ in the color of at least one bracket. As the result can be quite large, print it modulo1000000007 (109 + 7).

Input

The first line contains the single string s (2 ≤ |s| ≤ 700)
which represents a correct bracket sequence.

Output

Print the only number — the number of ways to color the bracket sequence that meet the above given conditions modulo 1000000007(109 + 7).

Sample test(s)

input

(())

output

12

input

(()())

output

40

input

()

output

4

Note

Let's consider the first sample test. The bracket sequence from the sample can be colored, for example, as is shown on two figures below.

The two ways of coloring shown below are incorrect.

/**
CF149D 区间dp
题目大意:给定一个有效的括号序列对于每个括号有三种涂色方法，涂红色或蓝色或不涂。而且相邻的两个括号不能涂同样的颜色（能够都不涂）
         对于每一对括号都要恰有一个括号涂色，问对于整个序列有多少涂色的方法
解题思路：dp[i][j][x][y]表示对于区间（i,j）左括号为x色，右括号为y色，有多少中情况。

对于区间（ij）若i和j是相应则转移到（i+1,j-1）若不正确应则转移到（i,p）*(p+1,j)当中p为i括号的相应点，详细转移请看代码
*/
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
typedef long long LL;
const LL mod=1e9+7;
char a[800];
int n,Hash[800],tmp[800];
LL dp[705][705][4][4];

void dfs(int l,int r)
{
    if(l+1==r)
    {
        dp[l][r][0][1]=1;
        dp[l][r][1][0]=1;
        dp[l][r][2][0]=1;
        dp[l][r][0][2]=1;
        return;
    }
    if(Hash[r]==l)
    {
        dfs(l+1,r-1);
        for(int i=0;i<3;i++)
        {
            for(int j=0;j<3;j++)
            {
                if(i!=1)
                    dp[l][r][1][0]=(dp[l][r][1][0]+dp[l+1][r-1][i][j])%mod;
                if(j!=1)
                    dp[l][r][0][1]=(dp[l][r][0][1]+dp[l+1][r-1][i][j])%mod;
                if(i!=2)
                    dp[l][r][2][0]=(dp[l][r][2][0]+dp[l+1][r-1][i][j])%mod;
                if(j!=2)
                    dp[l][r][0][2]=(dp[l][r][0][2]+dp[l+1][r-1][i][j])%mod;
            }
        }
    }
    else
    {
        int p=Hash[l];
        dfs(l,p);
        dfs(p+1,r);
        for(int i=0;i<3;i++)
        {
            for(int j=0;j<3;j++)
            {
                for(int x=0;x<3;x++)
                {
                    for(int y=0;y<3;y++)
                    {
                        if(!(x==1&&y==1||x==2&&y==2))
                            dp[l][r][i][j]=(dp[l][r][i][j]+(dp[l][p][i][x]*dp[p+1][r][y][j])%mod)%mod;
                    }
                }
            }
        }
    }
}
int main()
{
    while(~scanf("%s",a+1))
    {
        n=strlen(a+1);
        int k=0;
        memset(tmp,0,sizeof(tmp));
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=n;i++)
        {
            if(a[i]=='(')
            {
                tmp[k++]=i;
            }
            else
            {
                Hash[i]=tmp[k-1];
                Hash[tmp[k-1]]=i;
                k--;
            }
        }
        dfs(1,n);
        LL ans=0;
        for(int i=0;i<3;i++)
        {
            for(int j=0;j<3;j++)
            {
                ans=(ans+dp[1][n][i][j])%mod;
            }
        }
        printf("%lld\n",ans);
    }
    return 0;
}