php实现排列组合
php实现排列组合
一、总结
1、回溯:回溯的函数参数有些生疏了,记录递归的位置(pos或step),还要有东西(vis数组)来记录这个是否已经被访问
2、php全局变量的使用 :外部定义的普通变量,函数内部定义global
二、代码
需求:php实现排列组合
代码一:
/**
* 排列组合
* 采用二进制方法进行组合的选择,如表示5选3时,只需有3位为1就可以了,所以可得到的组合是 01101 11100 00111 10011 01110等10种组合
*
* @param 需要排列的数组 $arr
* @param 最小个数 $min_size
* @return 满足条件的新数组组合
*/
function pl($arr,$size=5) {
$len = count($arr);
$max = pow(2,$len);
$min = pow(2,$size)-1;
$r_arr = array();
for ($i=$min; $i<$max; $i++){
$count = 0;
$t_arr = array();
for ($j=0; $j<$len; $j++){
$a = pow(2, $j);
$t = $i&$a;
if($t == $a){
$t_arr[] = $arr[$j];
$count++;
}
}
if($count == $size){
$r_arr[] = $t_arr;
}
}
return $r_arr;
}
$pl = pl(array(1,2,3,4,5,6,7),5);
var_dump($pl);
代码二:
<?php
namespace app\index\controller; use app\index\controller\Base; class Exercise extends Base
{
public function index()
{
// return view('insert_array');
$this->plzhDemo();
} /**
* php实现排列组合
* 参数:传入数组 排列组合所取的位数 vis数组 ans数据用来记录每次的结果
* 算法;递归(回溯)
* 返回值:返回排列组合结果数组
* @return [type] [description]
*/
private $count1=0;
public function plzh($arr,$n,$pos,$vis,$ans){
//1、递归返回条件:位数够了就可以返回了
if($pos>$n-1){
global $count1;
$count1++;
dump($ans);
}else{
$len=count($arr);
for ($i=0; $i < $len; $i++) {
if($vis[$i]==0){//没取
$ans[$pos]=$arr[$i];
$vis[$i]=1;
$this->plzh($arr,$n,$pos+1,$vis,$ans);
$vis[$i]=0;
}
}
}
//2、递归里面的算法(一位一位的来取)取一位之后,把这一位的数标记置为已经取了,然后取后面的位的时候从没有取的数里面取,所以需要标记数组
//2.1、 从未取的数里面依次取一位就好 }
public function plzhDemo(){
$arr=array(1,2,3,4,5,6,7);
$n=5;
$vis=array();
for ($i=0; $i <=count($arr) ; $i++) {
$vis[$i]=0;
}
$ans=array();
$this->plzh($arr,$n,0,$vis,$ans);
global $count1;
dump($count1);
} }
截图:
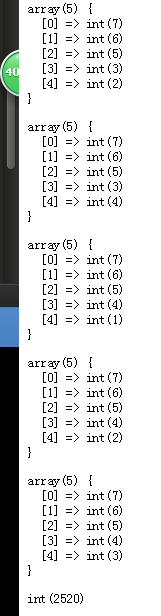
php实现排列组合的更多相关文章
- 学习sql中的排列组合,在园子里搜着看于是。。。
学习sql中的排列组合,在园子里搜着看,看到篇文章,于是自己(新手)用了最最原始的sql去写出来: --需求----B, C, F, M and S住在一座房子的不同楼层.--B 不住顶层.C 不住底 ...
- .NET平台开源项目速览(11)KwCombinatorics排列组合使用案例(1)
今年上半年,我在KwCombinatorics系列文章中,重点介绍了KwCombinatorics组件的使用情况,其实这个组件我5年前就开始用了,非常方便,麻雀虽小五脏俱全.所以一直非常喜欢,才写了几 ...
- 【原创】开源.NET排列组合组件KwCombinatorics使用(三)——笛卡尔积组合
本博客所有文章分类的总目录:本博客博文总目录-实时更新 本博客其他.NET开源项目文章目录:[目录]本博客其他.NET开源项目文章目录 KwCombinatorics组件文章目录: 1. ...
- 【原创】开源.NET排列组合组件KwCombinatorics使用(二)——排列生成
本博客所有文章分类的总目录:本博客博文总目录-实时更新 本博客其他.NET开源项目文章目录:[目录]本博客其他.NET开源项目文章目录 KwCombinatorics组件文章目录: 1. ...
- 【原创】开源.NET排列组合组件KwCombinatorics使用(一)—组合生成
本博客所有文章分类的总目录:本博客博文总目录-实时更新 本博客其他.NET开源项目文章目录:[目录]本博客其他.NET开源项目文章目录 KwCombinatorics组件文章目录: 1. ...
- hdu1521 排列组合(指数型母函数)
题意: 有n种物品,并且知道每种物品的数量ki.要求从中选出m件物品的排数. (全题文末) 知识点: 普通母函数 指数型母函数:(用来求解多重集的排列问题) n个元素,其中a1,a2, ...
- [leetcode] 题型整理之排列组合
一般用dfs来做 最简单的一种: 17. Letter Combinations of a Phone Number Given a digit string, return all possible ...
- 排列组合算法(PHP)
用php实现的排列组合算法.使用递归算法,效率低,胜在简单易懂.可对付元素不多的情况. //从$input数组中取$m个数的组合算法 function comb($input, $m) { if($m ...
- iOS多线程中,队列和执行的排列组合结果分析
本文是对以往学习的多线程中知识点的一个整理. 多线程中的队列有:串行队列,并发队列,全局队列,主队列. 执行的方法有:同步执行和异步执行.那么两两一组合会有哪些注意事项呢? 如果不是在董铂然博客园看到 ...
- leetcode-Combinations 复习复习排列组合
Combinations 题意: 根据给定的n和k,生成从1到n范围内长度为k的排列组合 示例: n=4 k=2 [[1, 2], [1, 3], [1, 4], [2, 1], [2, 3], [2 ...
随机推荐
- GenIcam标准介绍
GenICam TM的目标是为各种相机和设备提供通用编程接口.无论他们使用什么接口技术(GigE Vision,USB3 Vision,CoaXPress,Camera Link HS,Camera ...
- spring的PropertyPlaceholderConfigurer不生效的问题
经常出现这种问题,每次都debug知道原因,但每次都会忘记,所以记录一下. 原因:maven项目中使用了非maven管理的jar包(通过systemPath引用),这些jar包没有放在${projec ...
- [CSSinJS] Convert Sass (SCSS) Styled Button to CSSinJS with JavaScript Templates and Variables
This is an introduction to CSSinJS that doesn't require any JavaScript knowledge, just a basic CSS. ...
- 把握linux内核设计思想(三):下半部机制之软中断
[版权声明:尊重原创.转载请保留出处:blog.csdn.net/shallnet,文章仅供学习交流,请勿用于商业用途] 中断处理程序以异步方式执行,其会打断其它重要代码,其执行时该中 ...
- uva 473(dp)
题意:按创作时间给出n首歌每首歌的时间ti,然后按创作时间装到m个光盘内,给出光盘最大分钟数t,问m个光盘最多总共放多少首歌. 题解:对于每首歌都能够选或者不选,假设选择了这首歌,是否把这首歌当做第j ...
- (2) 我的结果- spec2006中精确的simulation points运行点
spec06中获取simpoints的环境说明: spec的版本号为spec2006v1.0; 使用ref input with runspec; 100millions为周期生成的simpoints ...
- SpringMVC 常见异常处理
1.javax.xml.bind.UnmarshalException: unexpected element (uri:"", local:"request" ...
- Spring MVC 待学习---新特性
Spring3.1新特性 一.Spring2.5之前,我们都是通过实现Controller接口或其实现来定义我们的处理器类. 二.Spring2.5引入注解式处理器支持,通过@Controller ...
- sql的四大函数
字符串函数: 1.charindex(字符串表达式 1, 字符串表达式2[,整数表达式]) select charindex('ab','BCabTabD')返回 3 select charindex ...
- 【Linux下用户和组管理】
创建用户--useradd . 命令格式:useradd [参数] 用户名 useradd也可写成adduser . 参数如下 -u 指定UID号 -d 指定宿主目录 -e 指定生效时间 -g 指定基 ...
