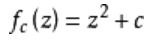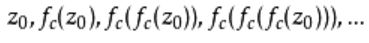OpenCV绘制朱利亚(Julia)集合图形
朱利亚集合是一个在复平面上形成分形的点的集合。以法国数学家加斯顿·朱利亚(Gaston Julia)的名字命名。
朱利亚集合可以由下式进行反复迭代得到:
对于固定的复数c,取某一z值(如z = z0),可以得到序列
这一序列可能反散于无穷大或始终处于某一范围之内并收敛于某一值。我们将使其不扩散的z值的集合称为朱利亚集合。
以下使用OpenCV编码绘制Julia集图形:
#include <Windows.h>
#include<highgui/highgui.hpp>
using namespace cv;
const int icount = 200; //迭代次数
const float c = -0.85; //实部
const float d = 0.088; //虚部
double m_real, m_image; //Mandelbro集
class ComplexClass
{
public:
double real;
double image;
ComplexClass(double r = 0, double i = 0) { real = r, image = i; }
};
ComplexClass operator+(const ComplexClass& a, const ComplexClass &b)
{
ComplexClass c;
c.real = a.real + b.real;
c.image = a.image + b.image;
return c;
}
ComplexClass operator*(const ComplexClass& a, const ComplexClass &b)
{
ComplexClass c;
c.real = a.real * b.real - a.image * b.image;
c.image = a.image * b.real + a.real * b.image;
return c;
}
double Model(ComplexClass a)
{
return sqrtf(a.real * a.real + a.image * a.image);
}
double Iteration(ComplexClass a, int n)
{
if (n == 0)
return Model(a);
else
{
ComplexClass temp = a*a;
temp.real += c;
temp.image += d;
// temp.real += m_real; 把这两句代替前面的两句就是mandelbrot集了
// temp.image += m_image;
return Iteration(temp, n - 1);
}
}
Vec3b dye(double dist)
{
if (dist < 1000000 && dist>-1000000)
return Vec3b(255, 0, 0);
else
return Vec3b(0, 0, 0); //Julia集之外的区域置为黑色
}
int main()
{
Mat image = Mat(Size(500, 500), CV_8UC3, Scalar::all(10));
for (int Y = 0; Y < image.rows; Y++)
{
for (int X = 0; X < image.cols; X++)
{
float x = (X - image.cols / 2) / 200.0;
float y = (Y - image.rows / 2) / 200.0;
m_real = x;
m_image = y;
ComplexClass a(x, y);
float dist = Iteration(a, icount);
image.at<Vec3b>(Y, X) = dye(dist);
}
}
//namedWindow("OpenCV For Julia", 0);
imshow("OpenCV For Julia | c = -0.85 d = 0.088", image);
waitKey();
}改变实部c和虚数b的值可以得到不同的图形,很漂亮。
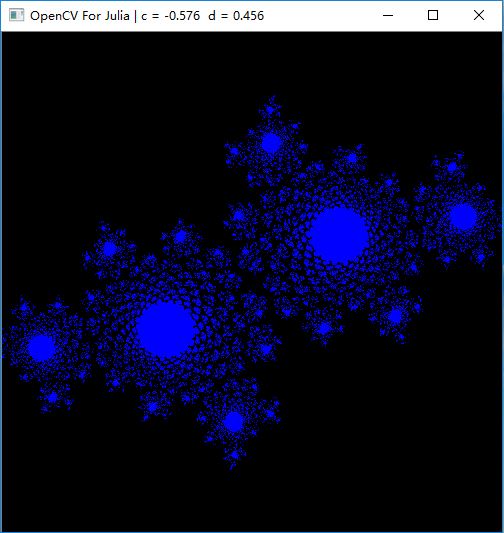
c=-0.576 d=0.456:
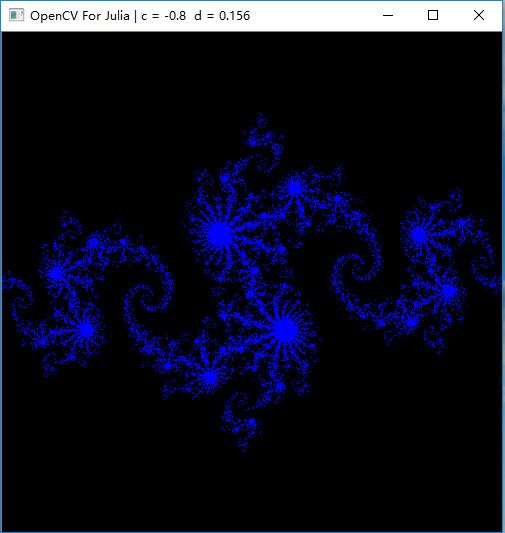
c=-0.8 d=0.156:
c=0.285 d=0.02:
c=-0.85 d=0.088:
OpenCV绘制朱利亚(Julia)集合图形的更多相关文章
- CUDA+OpenCV 绘制朱利亚(Julia)集合图形
Julia集中的元素都是经过简单的迭代计算得到的,很适合用CUDA进行加速.对一个600*600的图像,需要进行360000次迭代计算,所以在CUDA中创建了600*600个线程块(block),每个 ...
- 混沌分形之朱利亚集(JuliaSet)
朱利亚集合是一个在复平面上形成分形的点的集合.以法国数学家加斯顿·朱利亚(Gaston Julia)的名字命名.我想任何一个有关分形的资料都不会放过曼德勃罗集和朱利亚集.这里将以点集的方式生成出朱利亚 ...
- 详解用OpenCV绘制各类几何图形
摘要:本文详细介绍了OpenCV绘制几何图形的方法,利用cv2.line().v2.circle().cv2.rectangle().cv2.ellipse().cv2.polylines().cv2 ...
- Linux命令之dot - 绘制DOT语言脚本描述的图形
本文链接:http://codingstandards.iteye.com/blog/840055 用途说明 Graphviz (Graph Visualization Software的缩写)是一个 ...
- C# winform如何清除由Graphics类绘制出来的所有线条或图形
在C#winform应用程序中,可以用GDI绘制出线条或图形. 1.在主窗体上绘制线条或图形 using (Graphics g = this.CreateGraphics()) { ...
- Turtle绘制带颜色和字体的图形(Python3)
转载自https://blog.csdn.net/wumenglu1018/article/details/78184930 在Python中有很多编写图形程序的方法,一个简单的启动图形化程序设计的方 ...
- 绘制播放音乐时的音波图形的View
绘制播放音乐时的音波图形的View 这个效果类似于这个哦: 效果如下: 源码: MusicView.h 与 MusicView.m // // MusicView.h // Music // // C ...
- OpenCV绘制检测结果
OpenCV绘制检测结果 opencv rtcp timestamp 一.介绍 由于在验证阶段,使用FPGA时我们的算法检测速度很慢,没法直接在主流上进行绘图,否则的话,主流就要等待算法很久才能 ...
- [CTF]维吉尼亚密码(维基利亚密码)
[CTF]维吉尼亚密码(维基利亚密码) ----------------------百度百科 https://baike.baidu.com/item/维吉尼亚密码/4905472?fr=aladdi ...
随机推荐
- vue使用改变element-ui主题色
每个项目的主题色一般都不一样,直接用element-ui的默认主题色似乎有点不合适,还需要自己一个一个的找元素class名然后在修改样式,非常麻烦,还容易影响到包含该类名的其他元素样式,所以需要自定义 ...
- Google guava工具类的介绍和使用
概述 工具类 就是封装平常用的方法,不需要你重复造轮子,节省开发人员时间,提高工作效率.谷歌作为大公司,当然会从日常的工作中提取中很多高效率的方法出来.所以就诞生了guava.. 高效设计良好的API ...
- js和jquery实现页面滚动监听
js和jquery实现页面滚动监听 一.总结 一句话总结:onscroll方法和监听页面元素的高度都可以实现滚动监听. 1.onscroll方法实现滚动监听的核心代码是什么? <body ons ...
- 算法 Tricks(四)—— 判断序列中的字符/数值是否交替出现
比如:353, 54545,数字都是交替出现的: bool alternate = true; for (int i = 0; i < M.size(); ++i){ if (M[i] != M ...
- 【a903】石子归并
Time Limit: 10 second Memory Limit: 2 MB 问题描述 在一个圆形操场的四周摆放着N堆石子(N<= 100),现要将石子有次序地合并成一堆.规定每次只能选取相 ...
- Maven项目中mvn clean后找不到測试类问题
在Maven项目中进行单元測试,但mvn clean后又一次mvn install项目,再次进行单元測试.会有下面的错误. <span style="font-family:KaiTi ...
- Windows平台CUDA开发之前的准备工作
CUDA是NVIDIA的GPU开发工具,眼下在大规模并行计算领域有着广泛应用. windows平台上面的CUDA开发之前.最好去NVIDIA官网查看说明,然后下载对应的driver. ToolKits ...
- ios开发网络学习AFN框架的使用一:get和post请求
#import "ViewController.h" #import "AFNetworking.h" @interface ViewController () ...
- XML输出到浏览器报错
在使用Firefox浏览器测试我编写的xml文件时,遇到如下错误:我的xml源代码如下: <?xml version="1.0" encoding="UTF-8&q ...
- 【34.25%】【BZOJ 2648】SJY摆棋子
Time Limit: 20 Sec Memory Limit: 128 MB Submit: 2718 Solved: 931 [Submit][Status][Discuss] Descrip ...