dfs序七个经典问题（转）

我这个人不怎么喜欢写轻重链剖分和LCT 还是喜欢dfs序、括号序列之类的

毕竟线段树好写多了

然后就有了这篇转载的文章 写在这边以后有时间看看

原文链接：https://www.cnblogs.com/weeping/p/6847112.html

参考自：《数据结构漫谈》-许昊然

dfs序是树在dfs先序遍历时的序列，将树形结构转化成序列问题处理。

dfs有一个很好的性质：一棵子树所在的位置处于一个连续区间中。

ps:deep[x]为x的深度，l[x]为dfs序中x的位置，r[x]为dfs序中x子树的结束位置

1.点修改，子树和查询

　　在dfs序中，子树处于一个连续区间中。所以这题可以转化为：点修改，区间查询。用树状数组或线段树即可。

2.树链修改，单点查询

　　将一条树链x,y上的所有点的权值加v。这个问题可以等价为：

　　1）.x到根节点的链上所有节点权值加v。

　　2）.y到根节点的链上所有节点权值加v。

　　3）.lca（x,y）到根节点的链上所有节点权值和减v。

　　4）.fa(lca(x,y))到根节点的链上所有节点权值和减v。　　

　　上面四个操作可以归结为：节点x到根节点链上所有节点的权值加减v。修改节点x权值，当且仅当y是x的祖先节点时，x对y的值有贡献。

　　所以节点y的权值可以转化为节点y的子树节点贡献和。从贡献和的角度想：这就是点修改，区间和查询问题。

　　修改树链x,y等价于add(l[x],v),add(l[y],v),add(l[lca(x,y)],-v),add(l[fa(lca(x,y))],-v)。

　　查询：get_sum(r[x])-get_sum(l[x]-1)

　　用树状数组或线段树即可。

3.树链修改，子树和查询

　　树链修改部分同上一问题。下面考虑子树和查询问题：前一问是从贡献的角度想，子树和同理。

　　对于节点y其到根节点的权值和，考虑其子节点x的贡献：w[x]*(deep[x]-deep[y]+1) = w[x]*(deep[x]+1)-w[x]*deep[y]

　　所以节点y的子树和为：

　　

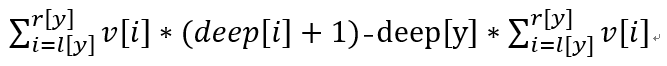
　　ps:公式中的v[i]为手误，应为w[i]。

　　所以用两个树状数组或线段树即可：

　　　　第一个维护∑w[i]*(deep[i]+1):支持操作单点修改，区间和查询。（这也就是问题2）

　　　　第二个维护∑ w[i]：支持操作单点修改，区间查询。（这其实也是问题2）

4.单点更新，树链和查询

　　树链和查询与树链修改类似，树链和(x,y)等于下面四个部分和相加：

　　1）.x到根节点的链上所有节点权值加。

　　2）.y到根节点的链上所有节点权值加。

　　3）.lca（x,y）到根节点的链上所有节点权值和的-1倍。

　　4）.fa(lca(x,y))到根节点的链上所有节点权值和的-1倍。

　　所以问题转化为：查询点x到根节点的链上的所有节点权值和。

　　修改节点x权值，当且仅当y是x的子孙节点时，x对y的值有贡献。

　　差分前缀和，y的权值等于dfs中[1,l[y]]的区间和。

　　单点修改：add(l[x],v),add(r[x]+1,-v);

5.子树修改，单点查询

　　修改节点x的子树权值，在dfs序上就是区间修改，单点权值查询就是单点查询。

　　区间修改，单点查询问题：树状数组或线段树即可;

6.子树修改，子树和查询

　　题目等价与区间修改，区间查询问题。用树状数组或线段树即可。

7.子树修改，树链查询

　　树链查询同上，等价为根节点到y节点的链上所有节点和问题。

　　修改节点x的子树权值，当且仅当y是x的子孙节点时（或y等于x），x对y的值有贡献。

　　x对根节点到y节点的链上所有节点和的贡献为：w[x]*(deep[y]-deep[x]+1)=w[x]*deep[y]-w[x]*(1-deep[x])

　　同问题三，用两个树状数组或线段树即可。