希尔伯特曲线——第八届蓝桥杯C语言B组（国赛）第三题

原创

---

标题：希尔伯特曲线

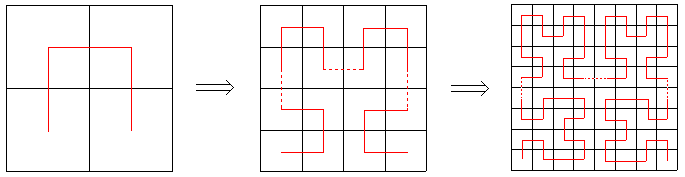
希尔伯特曲线是以下一系列分形曲线 Hn 的极限。我们可以把 Hn 看作一条覆盖 2^n × 2^n 方格矩阵的曲线，曲线上一共有 2^n × 2^n 个顶点(包括左下角起点和右下角终点)，恰好覆盖每个方格一次。

[p1.png]

Hn(n > 1)可以通过如下方法构造：
1. 将 Hn-1 顺时针旋转90度放在左下角
2. 将 Hn-1 逆时针旋转90度放在右下角
3. 将2个 Hn-1 分别放在左上角和右上角
4. 用3条单位线段把4部分连接起来

对于 Hn 上每一个顶点 p ，我们定义 p 的坐标是它覆盖的小方格在矩阵中的坐标(左下角是(1, 1)，右上角是(2^n, 2^n)，从左到右是X轴正方向，从下到上是Y轴正方向)，
定义 p 的序号是它在曲线上从起点开始数第几个顶点(从1开始计数)。

以下程序对于给定的n(n <= 30)和p点坐标(x, y)，输出p点的序号。请仔细阅读分析源码，填写划线部分缺失的内容。

#include <stdio.h>

long long f(int n, int x, int y) {
　　if (n == 0) return 1;
　　int m = 1 << (n - 1);
　　if (x <= m && y <= m) {
　　　　return f(n - 1, y, x);
　　}
　　if (x > m && y <= m) {
　　　　return 3LL * m * m + f(n - 1, ________________ , m * 2 - x + 1); // 填空
　　}
　　if (x <= m && y > m) {
　　　　return 1LL * m * m + f(n - 1, x, y - m);
　　}
　　if (x > m && y > m) {
　　　　return 2LL * m * m + f(n - 1, x - m, y - m);
　　}
}

int main() {
　　int n, x, y;
　　scanf("%d %d %d", &n, &x, &y);
　　printf("%lld", f(n, x, y));

　　return 0;
}

注意：只填写划线处缺少的内容，不要填写已有的代码或符号，也不要填写任何解释说明文字等。

（分别称下图三个网格称为A、B、C网格）

#include <stdio.h>

long long f(int n, int x, int y) {    //（x，y）只是用来判断在哪部分
    if (n == ) return ;
    int m =  << (n - );
    if (x <= m && y <= m) {    //左下角
        return f(n - , y, x);    //返回给上一层的是此点在此层的序号
    }
    if (x > m && y <= m) {    //右下角
        return 3LL * m * m + f(n - ,m+-y,  * m - x + ); //  填空
    }
    if (x <= m && y > m) {    //左上角
        return 1LL * m * m + f(n - , x, y - m);
    }
    if (x > m && y > m) {    //右上角
        return 2LL * m * m + f(n - , x - m, y - m);
    }
}

int main() {
    int n, x, y;
    scanf("%d %d %d", &n, &x, &y); //n为2的指数,(x,y)为顶点坐标
    printf("%lld", f(n, x, y));

    return ;
}
/*
得找出当前层的点对下一层相应点的映射关系
*/ 

答案：m+1-y

要明确的是：每个网格中的1*1的方格都对应曲线上的一个顶点——即使有些1*1的方格内不存在转折点，但也是曲线上的一个顶点。

    int m =  << (n - );
    /*
    左移1位相当于原数*2，左移2位相当于原数*pow(2,2);
    所以 m==1*pow(2,n-1);
    其实 m存储的就是边长为：pow(2,n) x pow(2,n) 的二分之一的长
    比如：输入的 n = 3，网格规模为8x8，则 m==4
    */

    if (x <= m && y <= m) {    //左下角
        return f(n - , y, x);    //返回给上一层的是此点在此层的序号
    }
    if (x > m && y <= m) {    //右下角
        return 3LL * m * m + f(n - ,m+-y,  * m - x + ); //  填空
    }
    if (x <= m && y > m) {    //左上角
        return 1LL * m * m + f(n - , x, y - m);
    }
    if (x > m && y > m) {    //右上角
        return 2LL * m * m + f(n - , x - m, y - m);
    }
    /*
    四个 if()中的 return 返回给上一层都是当前层顶点（x，y）的序号
    根据曲线的走势，左下角是序号的第一部分，其实是左上角、右上角、右下角
    比如我们要求左上角的顶点序号，所以我们应该要加上左下角的顶点数：1LL*m*m;
    要求右下角的顶点序号，要加上前面三部分（左下角、左上角、右上角）的顶点数：3LL * m * m
    XLL * m * m + f() (X=0/1/2/3,LL 代表长长整型) f()代表的是下一层传过来的点序号
    所以 '+' 左边的部分加上右边的部分==（x，y）的序号
    */

XLL * m * m + f（）中 f（）的两个参数的确定：

n-1传递给下一层，方便计算m，这里不解释；

另外两个参数分别对应下一层的（x，y），即用这层的 x’，y‘表示下一层的 x，y ；

左上角、右上角、左下角中的参数容易确定，我们用待定系数法来确定右下角的两个参数；

    if (x > m && y <= m) {    //右下角
        return 3LL * m * m + f(n - ,m+-y,  * m - x + ); //  填空
    }

由 2 * m - x + 1 可知下一层的 y 和当前层的 x 是相关联的；

所以推测下一层的 x 和当前层的 y 是相关联的；

设当前层的坐标为 （x'，y'），下一层的坐标为（x，y）； 

所以 y = 2 * m - x' + 1；即 x' = 2 * m - y + 1；（用下一层的坐标表示当前层的坐标）

可设 y’ = m*a + b*x + c；由于 m已知，所以可化简为 y' = b*x + F

我们从B、C两图中找出可以带入上式求出未知参数的坐标；

（1，1）——> （8，4）

（2，1）——> （8，3）

（3，1）——> （8，2）

左边的坐标从B图中任意取，右边的坐标要从C图的右下角部分取（我们的目标是右下角）；

比如B图中的序号为7的顶点的坐标为（2，4）；在C图右下角也找到序号为7的顶点，坐标为（5，3）；

将左边坐标的横坐标、右边坐标的纵坐标代入 y' = b*x + F 得：

4=b+F;

3=2b+F;

解得 b = -1，F=5；

所以 m*a+c=5；从 x' 的表达式很容易就可以推测出  F = m + 1；

当然，我这种是不严格的解题方法！

22:31:53

2018-05-08