POJ1054 The Troublesome Frog

题目来源：http://poj.org/problem?id=1054

题目大意：

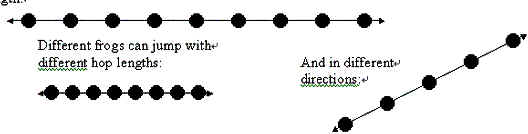
　　有一种青蛙在晚上经过一片稻田，在庄稼上跳跃，会把庄稼压弯。这让农民很苦恼。我们希望通过分析青蛙跳跃的路径，找出对稻田造成最大损害的青蛙。青蛙跳跃时总是沿着直线并且步长均匀，但不同青蛙可能步长或方向不一样。如下图所示：

　　稻田庄稼是均匀地种在矩形网格交点处的，如下左图所示。青蛙总是会完全穿过这片稻田，也就是说从稻田外跳入并最终跳出稻田。如下右图所示。

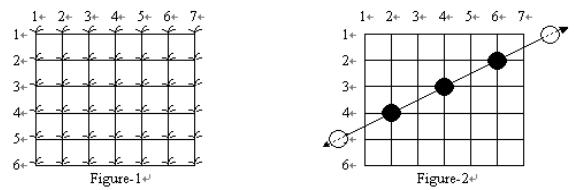
　　有许多青蛙会穿过这片稻田，从庄稼上跳跃。我们可以知道那些庄稼被青蛙“踩”过，有的庄稼可能被多只青蛙踩过。但是我们并不知道青蛙的路径是怎样的。也就是说对于下左图的青蛙路径，我们只能知道下右图中的青蛙脚印点坐标。

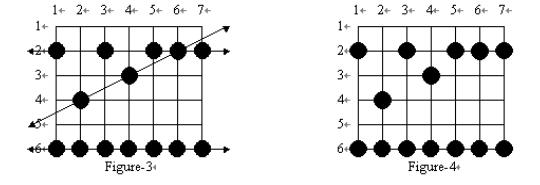
　　从Figure4，我们分析所有可能的青蛙路径，我们只关心脚印数大于3的路径，目标是找出所有可能的青蛙路径中脚印数最多的路径。Figure4对应的答案应该是7.

输入：第一行含两个整数R和C，表示稻田的行和列。1 <= R,C <= 5000.第二行为一个整数N，表示被压扁的庄稼数（即青蛙的脚印数），3 <= N <= 5000。接下来N行每行为一对整数，表示脚印坐标：行号r（1 <= r <= R）和列号c（1 <= c <= C），每个坐标只出现一次。

输出：一个整数表示穿过稻田留下脚印最多的青蛙的脚印数，如果找不到符合要求的青蛙路径输出0。

---

Sample Input

6 7
14
2 1
6 6
4 2
2 5
2 6
2 7
3 4
6 1
6 2
2 3
6 3
6 4
6 5
6 7

Sample Output

7

---

首先，暴力解决本题的思路是，遍历所有的脚印对，检查这两个脚印确定的直线可否穿过这对脚印形成青蛙路径，若可组成青蛙路径，记下路径的脚印数，然后找出路径上脚印数的最大值。这样做的问题是：一条路径上可能有很多点，那么每条路径都可能被计算多次，导致时间上的浪费。

可以用下面的方法来避免这个问题：我们假定青蛙在大方向上都是从稻田的一侧跳向另一侧，分别称为起点侧和终点侧。对于任意一条脚印路径，我们只在选取的脚印对（脚印对视为有序对，(i,j)和(j,i)为不同的脚印对）是路径上最靠近起点侧的两个脚印且i比j更靠近起点侧（或距离相等）时才检查一次这条路径（可以理解为 i 是青蛙跳进稻田第一步的脚印，j 是第二步的脚印），从而保证每条路径恰好被计算一次。

具体做法为：

首先，将所有脚印点进行排序。点的坐标(x, y), 排序策略为，首先按x由小到大排序，对于x相等的点再按列好从小到大排。

然后，对于排好序之后的脚印点，按顺序遍历脚印对时，假定第i个脚印点和第j个脚印点的坐标为(xi, yi), (xj, yj). 那么当 j > i 时，一定有xj >= xi。由前述的避免重复计算路径的策略，我们只计算所有的j>i的脚印对，即j一定是在经过i之后才到达的。

接下来，如何保证 i 和 j 恰好是最靠近起点侧的脚印（即青蛙跳进稻田后的第一步和第二步留下的脚印）？方法是：让青蛙“往回跳一步”，假定往回跳一步还在稻田内，那么有两种可能，一，回退一步的坐标是脚印点，那么这条直线可能形成路径，但不应该在遍历脚印点 i 和 j 时被计算，二，回退一步的坐标不是脚印点，那么这条直线不能穿过 i 和 j 形成青蛙路径，因为青蛙的步长是定值，无法直接从田外直接跳到 i。所以，只要青蛙回退一步的坐标仍然在田内，则这对脚印不可能符合要求，可以不用计算对应的路径。

再然后，并不是所有符合上面条件的 i 和 j 都会确定出一条可行的青蛙路径。（比如上面Figure4中的(2,2)和(3,4)，所在的直线就不能组成可行路径）。判断方法就是假设路径可行，由已知的两个点已经知道青蛙的步长和方向，模拟青蛙向前跳，如果青蛙恰好沿脚印点跳出稻田，说明路径可行，否则不可行。

至此似乎已经可以比较好的解决这个这个问题了，不过还有一些优化的策略：

1.由于青蛙沿直线跳跃且一定会穿越整片稻田，那么脚印数一定有一个上界--稻田的长和宽中的较大值。若已经有某条路径达到了上界，则不需要再搜索和计算。

2.当确定一对要检查的脚印对 i 和 j 后，我们是假定这条路径可行，那么我们已经知道了假定的路径中青蛙的步长、方向和起点，所以我们可以预测出该条路径的脚印点数，如果脚印数小于已找到的最大值，则没有必要再检查这对点对应的路径了。

3.我们在排序时不一定要固定按行排或按列排。按长度方向较小的方向为主序来排序可以使排序发挥更大的作用。

按照上述的各种策略课将题目由TLE加快到100ms内完成。

最后要注意需要输出0的情况。

 ///////////////////////////////////////////////////////////
 //        POJ1054 The Troublesome Frog
 //        Memory: 172K        Time: 63MS
 //        Language: C++        Result: Accepted
 //////////////////////////////////////////////////////////

 #include <cstdio>
 #include <cstdlib>

 using namespace std;

 struct Plant {
     int x, y;
 };

 Plant foot_print[];
 int r, c, n;
 int max_steps = ;

 int cmp_x(const void * a, const void * b) {
     Plant * pa = (Plant *) a;
     Plant * pb = (Plant *) b;
     if (pa->x == pb->x) {
         return pa->y - pb->y;
     } else {
         return pa->x - pb->x;
     }
 }

 int cmp_y(const void * a, const void * b) {
     Plant * pa = (Plant *) a;
     Plant * pb = (Plant *) b;
     if (pa->y == pb->y) {
         return pa->x - pb->x;
     } else {
         return pa->y - pb->y;
     }
 }

 int check_x(int j, int dx, int dy) {
     int ans = ;
     Plant plant;
     plant.x = foot_print[j].x + dx;
     plant.y = foot_print[j].y + dy;
     while (plant.x <= r && plant.y <= c && plant.y >= ) {
         if (bsearch(&plant, foot_print, n, sizeof(Plant), cmp_x)) {
             plant.x += dx;
             plant.y += dy;
             ++ans;
         } else {
             return ;
         }
     }
     return ans;
 }

 int check_y(int j, int dx, int dy) {
     int ans = ;
     Plant plant;
     plant.x = foot_print[j].x + dx;
     plant.y = foot_print[j].y + dy;
     while (plant.x >=  && plant.x <= r && plant.y <= c) {
         if (bsearch(&plant, foot_print, n, sizeof(Plant), cmp_y)) {
             plant.x += dx;
             plant.y += dy;
             ++ans;
         } else {
             return ;
         }
     }
     return ans;
 }

 int main(void) {
     scanf("%d%d%d", &r, &c, &n);
     for (int i = ; i < n; ++i) {
         scanf("%d%d", &foot_print[i].x, &foot_print[i].y);
     }
     if (r > c) {
         if (r > ) {
             qsort(foot_print, n, sizeof(Plant), cmp_x);
             for (int i = ; i < n - ; ++i) {
                 for (int j = i + ; j < n - ; ++j) {
                     int dx = foot_print[j].x - foot_print[i].x;
                     int dy = foot_print[j].y - foot_print[i].y;
                     int px = foot_print[i].x - dx;
                     int py = foot_print[i].y - dy;
                     if (px >=  && py >=  && py <= c) {
                         continue;
                     }
                     px = foot_print[i].x + max_steps * dx;
                     if (px > r) {
                         break;
                     }
                     py = foot_print[i].y + max_steps * dy;
                     if (py <  || py > c) {
                         continue;
                     }
                     int ans = check_x(j, dx, dy);
                     if (ans > max_steps) {
                         max_steps = ans;
                     }
                     if (max_steps == r) {
                         printf("%d\n", max_steps);
                         return ;
                     }
                 }
             }
         }
     } else if (c > ) {
         qsort(foot_print, n, sizeof(Plant), cmp_y);
         for (int i = ; i < n - ; ++i) {
             for (int j = i + ; j < n - ; ++j) {
                 int dx = foot_print[j].x - foot_print[i].x;
                 int dy = foot_print[j].y - foot_print[i].y;
                 int px = foot_print[i].x - dx;
                 int py = foot_print[i].y - dy;
                 if (px >=  && px <= r && py >= ) {
                     continue;
                 }
                 py = foot_print[i].y + max_steps * dy;
                 if (py > c) {
                     break;
                 }
                 px = foot_print[i].x + max_steps * dx;
                 if (px <  || px > r) {
                     continue;
                 }
                 int ans = check_y(j, dx, dy);
                 if (ans > max_steps) {
                     max_steps = ans;
                 }
                 if (max_steps == c) {
                     printf("%d\n", max_steps);
                     return ;
                 }
             }
         }
     }
     if (max_steps <= ) {
         max_steps = ;
     }
     printf("%d\n", max_steps);
     return ;
 }