洛谷P1033 自由落体

P1033 自由落体

题目描述

在高为 H 的天花板上有 n 个小球，体积不计，位置分别为 0，1，2，…．n-1。在地面上有一个小车（长为 L，高为 K，距原点距离为 S1）。已知小球下落距离计算公式为 d＝1/2*g*(t^2)，其中 g=10，t 为下落时间。地面上的小车以速度 V 前进。

如下图：

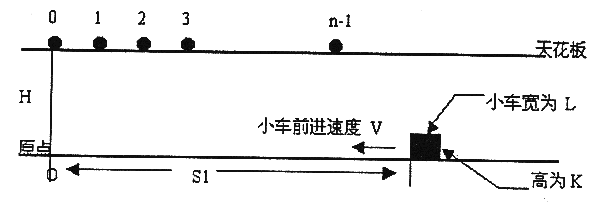
小车与所有小球同时开始运动，当小球距小车的距离 <= 0.0001(感谢Silver_N修正) 时，即认为小球被小车接受（小球落到地面后不能被接受）。

请你计算出小车能接受到多少个小球。

输入输出格式

输入格式：

键盘输人：

H，S1，V，L，K，n （l<=H，S1，V，L，K，n <=100000）

输出格式：

屏幕输出：

小车能接受到的小球个数。

输入输出样例

输入样例#1：

5.0 9.0 5.0 2.5 1.8 5

输出样例#1：

1

小球落到车上有一个时间范围，所以我们可以判断如果在范围内就可以落到车上

范围1：小球落到地面时，小车还未到达。此时小球的下落高度为h，经过的时间为t=sqrt(2*h/g)，那么小车在这段时间内走过的距离就是t*v，就可以算出小车与小球之间的距离，显然小车走的距离如果不能到达小球，小球就钓地上了

范围2：小车已经驶过，小球落到地上。此时小球下落高度以h-k计算，下落时间为sqrt(((h-k)*2)/g)，然后就和上边一样了

#include<iostream>
#include<cmath>
#include<cstdio>
#define g 10
using namespace std;
int main(){
    int n,x,ans=;
    double l,k,h,s1,t,v;
    cin>>h>>s1>>v>>l>>k>>n;
    for(int i=;i<=n-;i++){
        if(sqrt(*h/g)*v>=(s1-i-0.0001)&&sqrt(((h-k)*)/g)*v<=(s1-i+l+0.0001))
            ans++;
    }
    cout<<ans;
    return ;
}