P1447 [NOI2010]能量采集

题目描述

栋栋有一块长方形的地，他在地上种了一种能量植物，这种植物可以采集太阳光的能量。在这些植物采集能量后，栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。

栋栋的植物种得非常整齐，一共有n列，每列有m棵，植物的横竖间距都一样，因此对于每一棵植物，栋栋可以用一个坐标(x, y)来表示，其中x的范围是1至n，表示是在第x列，y的范围是1至m，表示是在第x列的第y棵。

由于能量汇集机器较大，不便移动，栋栋将它放在了一个角上，坐标正好是(0, 0)。

能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物，则能 量的损失为2k + 1。例如，当能量汇集机器收集坐标为(2, 4)的植物时，由于连接线段上存在一棵植物(1, 2)，会产生3的能量损失。注意，如果一棵植物与能量汇集机器连接的线段上没有植物，则能量损失为1。现在要计算总的能量损失。

下面给出了一个能量采集的例子，其中n = 5，m = 4，一共有20棵植物，在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。

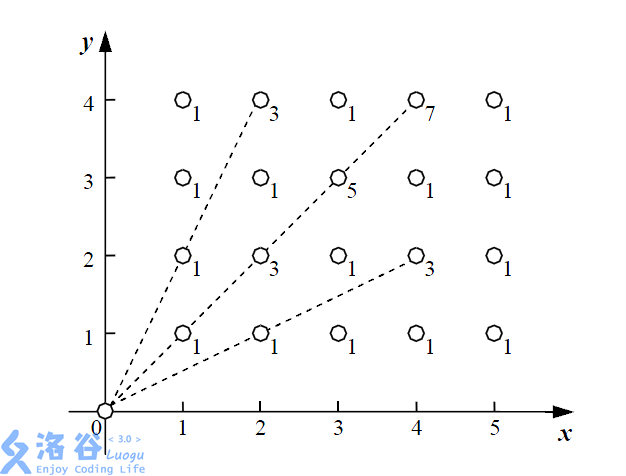
在这个例子中，总共产生了36的能量损失。

输入输出格式

输入格式：

仅包含一行，为两个整数n和m。

输出格式：

仅包含一个整数，表示总共产生的能量损失。

输入输出样例

输入样例#1：

5 4

输出样例#1：

36

输入样例#2：

3 4

输出样例#2：

20

说明

对于10%的数据：1 ≤ n, m ≤ 10；
对于50%的数据：1 ≤ n, m ≤ 100；
对于80%的数据：1 ≤ n, m ≤ 1000；
对于90%的数据：1 ≤ n, m ≤ 10,000；
对于100%的数据：1 ≤ n, m ≤ 100,000。

Solution：

　　本题zyys。

　　我们首先对图进行下分析，不难发现本题所求的是：$\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}{gcd(i,j)\times 2 - 1}$。

　　直接暴力枚举显然行不通，但是不难发现，同一最小公约数$x$可能会出现多次，于是我们考虑求满足$i\leq n,j\leq m$的$gcd(i,j)=x$的个数$f[x]$，那么$x$对答案的贡献就是$f[x]\times (x\times 2 -1)$。

　　那么显然$1\leq gcd(i,j)\leq min(n,m)$，直接枚举每个最小公约数$x$，那么$n$内的是$x$的倍数的数至少有$\lfloor{n/x}\rfloor$个，同理$m$内有$\lfloor{m/x}\rfloor$个，那么$x$作为公约数的数对共$\lfloor{n/x}\rfloor\times \lfloor{m/x}\rfloor$个，由于要求的是最小公约数$x$，显然上述数对中存在最小公约数为$x$倍数的数对，所以我们由容斥原理直接从上面的数对中减去最小公约数为$2\times x,3\times x,…k\times x\;,k\times x\leq min(n,m)$的数对个数。

　　由于上面$x$的倍数都大于$x$，可以在枚举$x$之前处理，直接倒序循环就好了。

　　最后统计累加答案。显然时间复杂度为调和级数，$O(n\log n)$。

代码：

#include<bits/stdc++.h>
#define il inline
#define ll long long
#define For(i,a,b) for(ll (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(ll (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=;
ll n,m,f[N],ans;

il int gi(){
    int a=;char x=getchar();
    while(x<''||x>'')x=getchar();
    while(x>=''&&x<='')a=(a<<)+(a<<)+x-,x=getchar();
    return a;
}

int main(){
    n=gi(),m=gi();
    if(n>m)swap(n,m);
    Bor(i,,n){
        f[i]=(n/i)*(m/i);
        for(ll j=;j*i<=n;j++)f[i]-=f[i*j];
        ans+=f[i]*(i*-);
    }
    cout<<ans;
    return ;
}