机器学习 (二) 多变量线性回归 Linear Regression with Multiple Variables

文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程，本文是针对该课程的个人学习笔记，如有疏漏，请以原课程所讲述内容为准。感谢博主Rachel Zhang 的个人笔记，为我做个人学习笔记提供了很好的参考和榜样。

---

§ 2. 多变量线性回归 Linear Regression with Multiple Variables

1 多特征值(多变量) Multiple Features(Variables)

首先，举例说明了多特征值(多变量)的情况。在下图的例子中，$x_1,x_2,x_3,x_4$都是输入的变量，因为变量个数大于一，所以也称为多变量的情况。

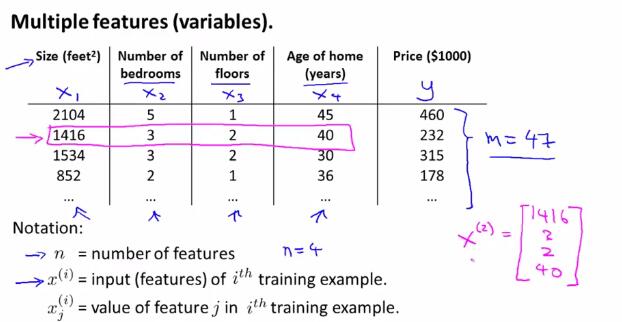
于是引出多变量线性回归的一般假设形式：

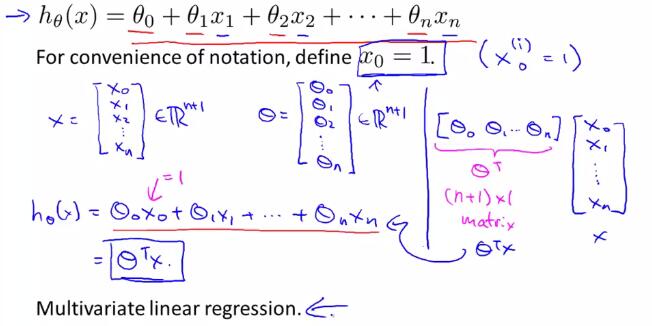
 2 多变量线性回归中的梯度下降法(gradient descent for multiple variables)

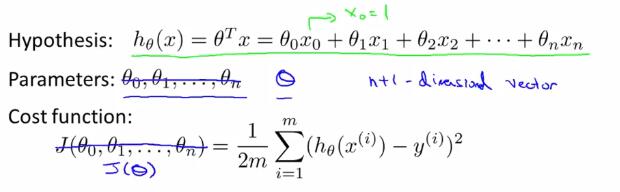
在以上的假设形式中，我们把$\theta$看成是一个$n+1$维的向量，把$J$看成是一个带有$n+1$维向量的函数。

下面的习题检测了对概念的理解：(1 注意$\sum$的位置 2 注意开始累加的位置)

将单变量与多变量线性回归中的梯度下降法作出比较：

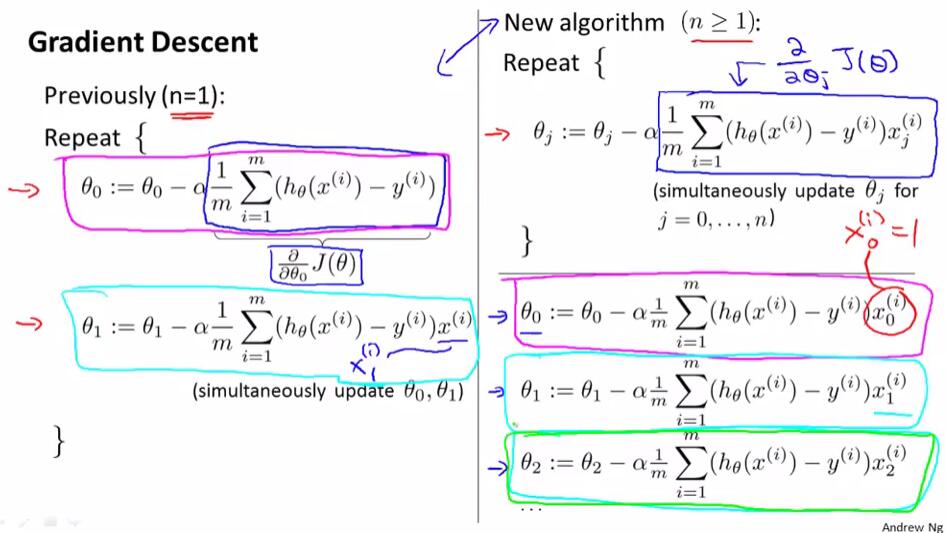
3 特征缩放 Feature scaling

如果不同变量之间的取值范围差别较大，使用梯度下降法时可能会花费较长时间、反复来回震荡。面对这种由于不同变量之间取值范围差别较大的所导致的问题，我们引入特征缩放(feature scaling)的方法来解决。

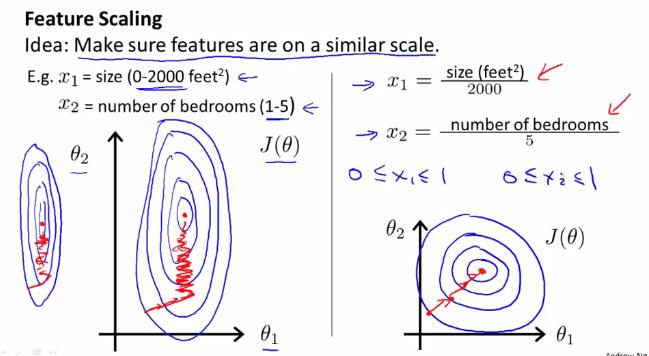
特征缩放(feature scaling) 使得数据特征调整到一定的范围内，比如[-1,1]之间。当然，这只是要求数据特征调整到一个大概的范围，具体实现的时候只要差不多即可，不一定要完全符合[-1,1]的范围。例如以下几种，就分别是正确或错误的特征缩放范围：

均值归一化(Mean normalization)处理：用$\frac{x_i-\mu_{i}}{\sigma}$取代$x_i$，或是简便地用$\frac{x_i-\mu_{i}}{max-min}$取代$x_i$。

下题考察了上述知识点的应用：

4 梯度下降法的应用 - 学习速率 Gradient Descent in practice  - Learning Rate

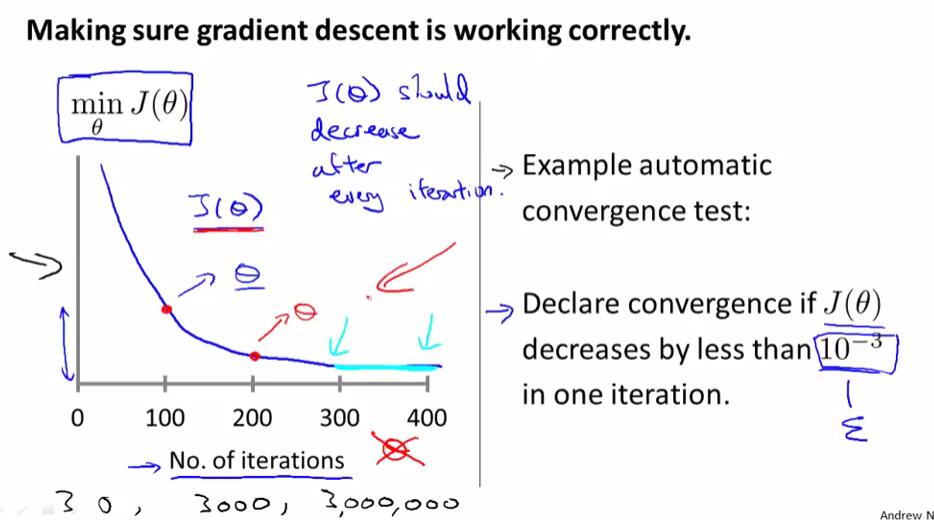
下图左边是以迭代次数为横轴，迭代指定次数以后得出的$\theta$对应$J(\theta)$的值为纵轴绘制的函数图像。如果梯度下降算法正常工作，那么每一步迭代之后，$J(\theta)$的值都应该减小。对于不同的问题，梯度下降算法所需的迭代次数可能会相差很大。

我们可以依靠自动收敛测试来判断是否正确收敛，但通常我们很难确定其临界值，因此实际中更多是使用$J(\theta)$关于迭代次数的函数图像来判断的。

当$J(\theta)$关于迭代次数的函数图像呈现如下图所示的递增或是“先下降后上升，再下降再上升……”时，我们可以使用一个更小的$\alpha$使得梯度下降算法正确工作。对于一个正确的$\alpha$而言，$J(\theta)$在每次迭代后都会下降；但如果$\alpha$太小，那么梯度下降算法将会收敛得很慢。

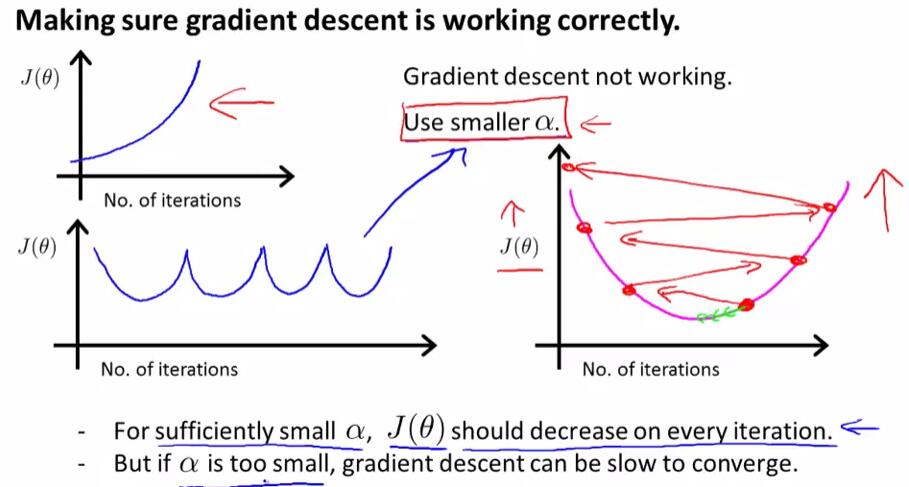
下题考察了上述知识点：(1) $\alpha$过大时，$J(\theta)$可能不会在每次迭代后减少 (2) $\alpha$太小的时候，梯度下降法的收敛速度会变慢

在选择学习速率时，我们一般以约3倍递增的形式，寻找能够正确收敛并且速度不会太慢的学习速率，使之尽可能快且正确地收敛。

5 特征与多项式回归 Features and polynomial regression

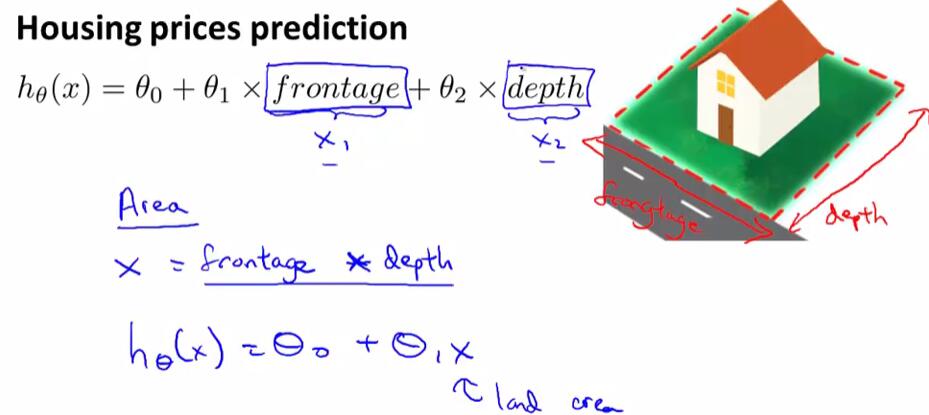
有时候，我们可以通过定义一个新的特征来优化模型，例如在房价预测模型中，定义一个新的$Area$使得$Area=frontage*depth$来优化模型。

对于多项式回归，可能会有不同的模型可供选择。要使得模型与数据能够拟合，我们可以参考以下方法做出修改来实现。如果使用梯度下降法，就要注意对数据特征进行缩放处理，使其具有可比性。

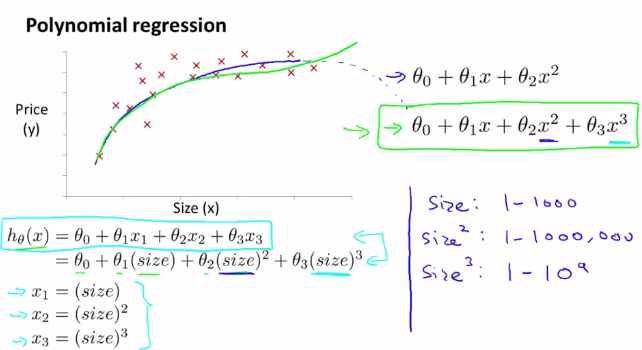
同时，还要注意对特征的选择，并且通过设计不同的特征，使得可以用更加复杂的函数去拟合数据。

例如在对房价数据的分析中，如果选择二次模型作为假设，二次函数最后会下降，但实际中房价不会随着房子面积的增长而下降，因此二次模型不是一个理想的模型。于是引入以下的模型：

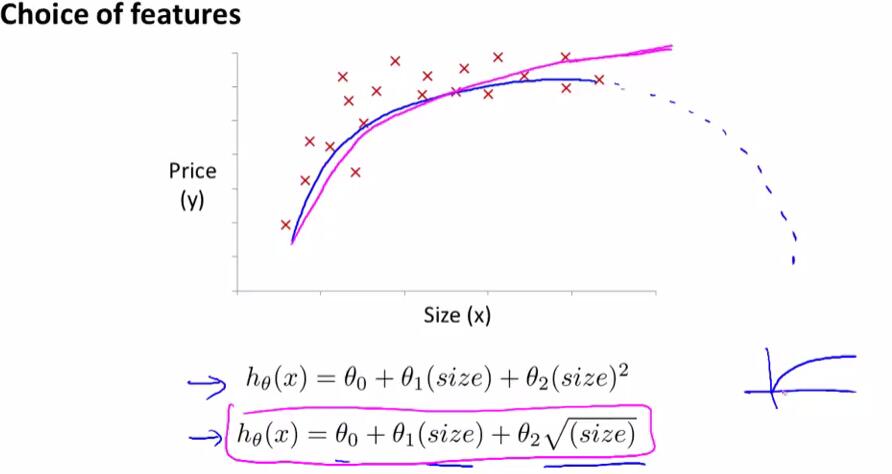
下题考察了特征缩放：

6 正规方程 Normal Equation

在训练集中加上一列对应特征变量$x_0$，然后构造矩阵$X,y$，然后得出使得$J(\theta)$最小的$\theta$：

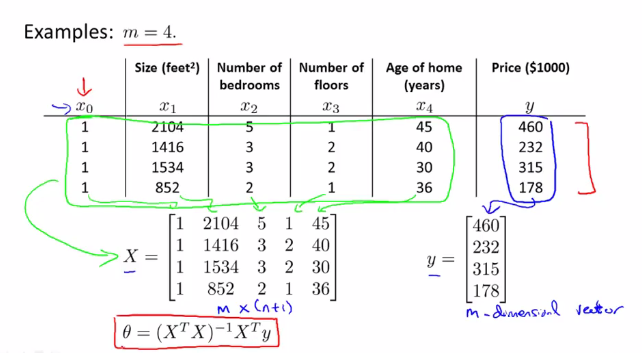
具体推广后的构造方法如下：

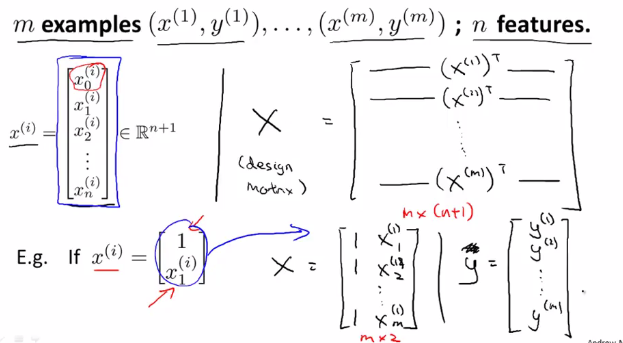
当使用正规方程法时，不需要特征变量归一化或是特征缩放。

下面介绍了梯度下降法与正规方程法各自的优劣及适用范围：

7 正规方程的不可逆性 Normal Equation Noninvertibility

利用pinv可以计算出$\theta$的值，即使$(X'X)$是不可逆的。

当$(X'X)$不可逆时，可能有两种原因：1 有多余的特征(互为线性函数) 2 特征过多。

解决方法：1 删除多余特征 2 用较少的特征尽可能反应较多的内容或使用正则化(regulation)方法

---

笔记目录

(一)单变量线性回归 Linear Regression with One Variable

(二)多变量线性回归 Linear Regression with Multiple Variables

(三)逻辑回归 Logistic Regression

(四)正则化与过拟合问题 Regularization/The Problem of Overfitting

(五)神经网络的表示 Neural Networks:Representation

(六)神经网络的学习 Neural Networks:Learning

(七)机器学习应用建议 Advice for Applying Machine Learning

(八)机器学习系统设计Machine Learning System Design

(九)支持向量机Support Vector Machines

(十)无监督学习Unsupervised Learning

(十一)降维 Dimensionality Reduction

(十二)异常检测Anomaly Detection

(十三)推荐系统Recommender Systems

(十四)大规模机器学习Large Scale Machine Learning