[HNOI2012]三角形覆盖问题

题面

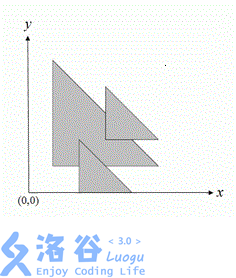
二维平面中，给定 \(N\) 个等腰直角三角形（每个三角形的两条直角边分别平行于坐标轴，斜边从左上到右下）。我们用三个非负整数 \((x, y, d)\) 来描述这样一个三角形，三角形三个顶点的坐标分别为 \((x, y), (x + d, y)\) 和 \((x, y + d)\) 。要求计算这 \(N\) 个三角形所覆盖的总面积。例如，下图有 \(3\) 个三角形，覆盖的总面积为 11.0。

输入格式：

输入文件第一行为一个正整数N，表示三角形的个数。

接下来的 \(N\) 行每行有用空格隔开的三个非负整数，\(x, y, d\) ，描述一个三角形的顶点坐标，分别为 \((x, y)\) , \((x + d, y)\) , \(( x, y+d)\) ，其中 \(x, y, d\) 满足 \(0<= x, y, d<=1000000\) 。

输出格式：

仅包含一行，为一个实数 \(S\) ，表示所有三角形所覆盖的总面积，输出恰好保留一位小数。输入数据保证 \(S\le 2^{31}\) 。

输入样例

3
1 1 4
2 0 2
3 2 2

输出样例

11.0

\(Solution:\)

显然扫描线，扫描线的做法因题而异，不同的题面有不同的写法。

这里给出链表+扫描线的方法：

先按 \(y\) 轴排序，然后从下扫描到上，因为坐标都是小于1e6的，所以直接暴力扫。

这题跟矩形面积并不一样，因为是等腰直角三角形，每次扫描线向上走一个单位，扫描线对应的地方覆盖就要少一。

数据结构：

1. 双向链表

实际上是一个容器，存的是覆盖当前扫描线的三角形的编号，即如果编号为 \(i\) 的三角形覆盖了扫描线的一部分，那么 \(list[i]\) 就在链表中。

链表只是为了我们快速修改信息，插入和删除都是 \(O(1)\) 的， 查询信息也很方便。

1. \(cover[x]\)

存储 ( \(x\) , 扫描线位置) 被多少个三角形覆盖，用来更新扫描线被覆盖的线段长度用。

算法流程：

1. 按 \(y\) 轴排序。
2. 从下往上扫描 \(i\) 记录扫描线的位置，\(j\) 记录当前有前 \(j\) 个在链表中或者已经处理完。
3. 先统计链表中的答案 \(now\) ，并修改信息，记下 \(i-1\) 时的覆盖线段长，\(ans+= \frac{now+last}{2}\).
4. 将新的三角形插进链表，更新 \(cover\) ，求出新的被覆盖线段长，记录到 \(last\) ，扫描线上移，执行 \(3\) 直至扫描完成。

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5 + 20;

int n, mx;
struct Tri
{
    int x, y, d, l, r;

    Tri() {}
    Tri(const int &_x, const int &_y, const int &_d)
    { x = _x, y = _y, d = _d, l = _x, r = _x + _d - 1;} 

} tri[N];
inline bool cmp(const Tri &A, const Tri &B)
{ return A.y < B.y; }

namespace List
{
    int head, tail, nxt[N], pre[N];

    void Del(int x)
    {
        pre[nxt[x]] = pre[x];
        nxt[pre[x]] = nxt[x];
    }

    void Ins(int x, int y)
    {
        pre[nxt[x]] = y;
        nxt[y] = nxt[x];
        nxt[x] = y;
        pre[y] = x;
    }

    bool ins(int x)
    {
        if (tri[x].d == 0) return false;
        Ins(head, x);
        return true;
    }
}
using namespace List;

int cover[(int)2e6 + 2];

int main()
{

    cin >> n;
    for (int i = 1; i <= n; ++ i)
    {
        int x, y, d;
        cin >> x >> y >> d;
        mx = max(mx, y + d);
        tri[i] = Tri(x, y, d);
    }
    sort(tri + 1, tri + 1 + n, cmp);

    head = 0; tail = n + 1;
    nxt[head] = tail; pre[tail] = head;
    int ans = 0, last = 0, now = 0;
    for (int i = tri[1].y, j = 1; i <= mx; ++ i)
    {
        now = last;
        for (int k = nxt[head]; k != tail; k = nxt[k])
        {
            -- cover[tri[k].r];
            if (!cover[tri[k].r]) now--;
            tri[k].r --;
            if (tri[k].x > tri[k].r) Del(k);
        }
        ans += now + last;
        while (j <= n && tri[j].y == i)
        {
            if (ins(j))
            {
                for (int k = tri[j].x; k < tri[j].x + tri[j].d; k ++)
                {
                    if (!cover[k]) now ++;
                    cover[k] ++;
                }
            }
            j ++;
        }
        last = now;
    }
    printf("%.1f\n", ans / 2.0);
}