ARC076 F Exhausted? Hall定理 + 线段树扫描线

～～～题面～～～

题目大意：

　　有n个人，m个座位，每个人可以匹配的座位是[1, li] || [ri, m],可能有人不需要匹配座位（默认满足），问最少有多少人不能被满足。

题解：

　　首先可以看出这是一个二分图匹配，根据hall定理，我们只需要求出max(人的子集大小 -  被选出的人可以选的座位集合大小）。

　　但是枚举人的复杂度太高，所以考虑枚举座位集合，因为每个人的可选区间都是一段前缀or后缀，因此要表达一个合法的座位集合，我们只需要所有人中最右边的li和最左边的ri即可。

　　如图所示：

　　

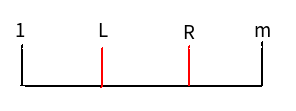
　　因此这个时候要使得尽可能接近max，就要把所有可选区间不超过我们当前枚举的区间的人都加进来。

　　可以使用扫描线，求出对于每个R，所有的L相对应的值。

　　

 #include<bits/stdc++.h>
 using namespace std;
 #define R register int
 #define AC 400100
 #define ac 1601000//error!!!数据范围是2 00000, 不是1开头！！！

 int n, m, ans = -INT_MAX, w;
 int Head[AC], Next[ac], date[ac], tot;
 int tree[ac], lazy[ac], l[ac], r[ac], l_[AC], r_[AC];

 inline int read()
 {
     int x = ;char c = getchar();
     while(c > '' || c < '') c = getchar();
     while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
     return x;
 }

 inline void add(int f, int w)
 {
     date[++tot] = w, Next[tot] = Head[f], Head[f] = tot;
 }

 inline void upmax(int &a, int b)
 {
     if(b > a) a = b;
 }

 void pre()
 {
     n = read(), m = read();
     for(R i = ; i <= n; i ++)
         l_[i] = read(), r_[i] = read(), add(r_[i], i);
 }

 inline void pushdown(int x)
 {
     if(lazy[x])
     {
         int ll = x * , rr = ll + ;
         lazy[ll] += lazy[x], lazy[rr] += lazy[x];
         tree[ll] += lazy[x], tree[rr] += lazy[x];//这里因为是+=，所以必须用lazy[x]，不然会将lazy[ll]中的一些东西重复统计
         lazy[x] = ;//最后才清空！！！！！！！！！！
     }//error!!!是区间加，不是赋值，不能直接覆盖，要+=
 }

 inline void update(int x)
 {
     tree[x] = max(tree[x * ], tree[x *  + ]);
 }

 void build(int x, int ll, int rr)
 {
     l[x] = ll, r[x] = rr;
     if(ll == rr)
     {
         tree[x] = -ll + ;
         return ;
     }
     int mid = (ll + rr) >> ;
     build(x * , ll, mid);
     build(x *  + , mid + , rr);
     update(x);
 }

 void change(int x, int ll, int rr)
 {
     pushdown(x);
     if(l[x] == ll && r[x] == rr)
     {
         lazy[x] += w, tree[x] += w;
         return ;
     }
     int mid = (l[x] + r[x]) >> ;
     if(rr <= mid) change(x * , ll, rr);
     else if(ll > mid) change(x *  + , ll, rr);
     else
     {
         change(x * , ll, mid);
         change(x *  + , mid + , rr);
     }
     update(x);
 }

 void find(int x, int ll, int rr)
 {
     pushdown(x);
     if(l[x] == ll && r[x] == rr)
     {
         upmax(ans, tree[x]);
         return ;
     }
     int mid = (l[x] + r[x]) >> ;
     if(rr <= mid) find(x * , ll, rr);
     else if(ll > mid) find(x *  + , ll, rr);
     else find(x * , ll, mid), find(x *  + , mid + , rr);//这是取max啊，，，，
 }

 void work()
 {
     int now;
     ans = n - m;//r = 0的情况
     for(R i = Head[m + ]; i; i = Next[i])
     {
         now = date[i], w = ;
         change(, l_[now] + , m + );
         //find(1, 4, 4);
     }
     //find(1, 4, 4);
     upmax(ans, tree[]);
     for(R i = m; i; -- i)
     {
         w = -;
         change(, , i + );
         for(R j = Head[i]; j; j = Next[j])
         {
             now = date[j], w = ;
             change(, l_[now] + , i + );
         }
         find(, , i + );//左端点在后面就不合法了
     }
     printf("%d\n", ans);
 }

 int main()
 {
     freopen("in.in", "r", stdin);
     pre();
     build(, , m + );//要多出一位来代表左端点取0的情况
     work();//ri最大居然可以到m+1...
     fclose(stdin);
     return ;
 }