∆ (triangle)

2.1 题目描述

给定一个无自环重边的无向图，求这个图的三元环1的个数以及补图2的三元环个数。

2.2 输入格式

第一行 2 个数 n, m ，分别表示图的点数、边数。

接下来 m 行，每行两个数 u, v ，表示一条连接 u, v 的无向边。

2.3 输出格式

一行两个数，依次表示原图的三元环个数以及补图的三元环的个数。

2.4 样例输入

5 5

1 2

1 3

2 3

2 4

3 4

2.5样例输出

2 1

2.6数据范围

对于 30% 的数据：n ≤ 100

对于 60% 的数据：m ≤ 500

对于 100% 的数据：n ≤ 10^5 , m ≤ 10^5

2.7评分方式

如果你两个数均输出正确，得 10 分。

否则如果两个数中任意一个正确或者两个数的和正确，得 6 分。 否则不得分。

注：

1大小为 3的环。即一个无序三元组 (x, y, z) 使得任意两点之间都有边

2一条连接(u, v)(u = v) 的边，如果在原图中出现了，那么在补图中不会出现，否则一定会在补图中出现。

题解：

题目中说两个数的和正确可以得分，是不是说明先求和是一个突破口呐？

对于一个完全图，三元环的数量是C(n,3)，少了一些边，就少了一些三元环，少的三元环应该有至少一条边在原图中，至少一条边在补图中。

减少的三元环数量为：sigma(d[i]*(n-1-d[i]))/2 (d[i]为度数)

一开始我想不通为什么是除以2，然后我画了两个图，就发现了答案，每个三元环可以被两个点找到。

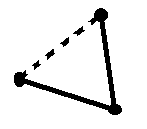
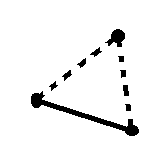
剩下的就是求原图中的三元环，有一个神奇的算法，和分段暴力有一丢丢类似吧。

将所有点分成两类:d[i]<sqrt(m)的和d[i]>sqrt(m)的.

先求包含第一类点的三元环个数. 由于边很少,所以枚举2条边即可.由于一个点的度不超过sqrt(m),所以一条边最多被枚到(sqrt(m))次,最多枚M条边,所以这个操作时O(m*sqrt(m))的.

再求不包含第一类点的三元环个数. 由于每条边贡献2个度,所以二类点的数量是O(sqrt(m))级的.直接枚举三个点,复杂度O((sqrt(m))^3)=O(m*sqrt(m))

所以算法总的复杂度是O(m*sqrt(m))的.

我先用了一个vector来判断点i与j是否有边，但是T掉了，然后get到了一个聪明的把一条边的两个节点一起hash的方法，就写了一个hash表水过去了。

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<set>
#define nn 100010
#define mod 1000007
#define base 2333
using namespace std;
namespace fastIO
{
#define buf_size 100000
    bool error;
    inline char gc()
    {
        static char buf[buf_size + 1],*l=buf,*r=buf;
        if(l==r)
        {
            l=buf;
            r=buf+fread(buf,1,buf_size,stdin);
            if(l==r) {error = 1;return -1;}
        }
       return *l++;
    }
    inline bool blank(char ch) {return ch=='\n'||ch =='\t'||ch ==' '||ch =='\r'||error;}
    inline bool getint(int &x)
    {
        char ch; int f = 1;
        while (blank(ch = gc())); if (error) return false;
        x = 0;
        if (ch == '-') f=-1,ch=gc();
        while (1){x = (x<<1) + (x<<3)+ch-'0';if(!isdigit(ch = gc())) break;}
        x*=f;
        return true;
    }
    inline void putint(long long x)
    {
        if(!x) {putchar('0'); return;}
        if(x<0){x=-x; putchar('-');}
        static int out[13];
        register int len = 0;
        while(x){out[++ len]=x%10; x/=10;}
        while(len) putchar(out[len --]+'0');
    }
#undef buf_size
}
using namespace fastIO;
int in[nn],fir[nn],nxt[nn<<1],to[nn<<1],a[1000007],b[1000007],head[1000007],next[1000007];
bool hash[1000007];
int e=0,inum=0;
void add(int u,int v)
{
	nxt[++e]=fir[u];fir[u]=e;to[e]=v;
	nxt[++e]=fir[v];fir[v]=e;to[e]=u;
}
long long c(long long n,int m)
{
	long long an=(n-2)*(n-1)*n/6;
	return an;
}
void addd(int u,int v)
{
    int t=(u*base+v)%mod;
    a[++inum]=u;b[inum]=v;next[inum]=head[t];head[t]=inum;
  }
inline bool query(int u,int v)
{
    int t=(u*base+v)%mod;
    for (int p=head[t];p;p=next[p])
      if (a[p]==u&&b[p]==v)
    return 1;
    return 0;
  }
int main()
{
	freopen("triangle.in","r",stdin);
	freopen("triangle.out","w",stdout);
	int n,m,u,v;
	getint(n);getint(m);
	long long all=0,sum=0;
	for(register int i(1);i<=m;i++)
	{
		getint(u);getint(v);
		addd(u,v);
		add(u,v);
		in[u]++;in[v]++;
	}
	for(register int i(1);i<=n;i++)
	  all+=in[i]*(n-1-in[i]);
	all/=2;
	all=c(n,3)-all;
	for(register int i(1);i<=n;i++)
	{
		for(register int j=fir[i];j;j=nxt[j])
		  for(register int k=nxt[j];k;k=nxt[k])
		  {
		  	if(query(to[j],to[k])||query(to[k],to[j]))
		  	  sum++;
		  }
	}
	putint(sum/3);putchar(' ');putint(all-sum/3);
	return 0;
}