luogu P4018 Roy&October之取石子（博弈论）

题意

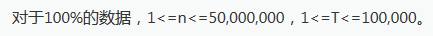
题解

如果n是6的倍数，先手必败，否则先手必胜。

因为6*x一定不是p^k

所以取得话会变成6*y+a的形式a=1，2，3，4，5；

然后a一定为质数。我们把a取完就又成为了6*x的形式。

又因为总数不断减少，所以6*x的局面是必败局面。

做完这题让我想起了初中时就被这种问题被人坑过。

然后博弈论可以先把SG的表打出来。

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int t,n;
 int main(){
     scanf("%d",&t);
     while(t--){
         scanf("%d",&n);
         if(n%==)printf("Roy wins!\n");
         else printf("October wins!\n");
     }
     return ;
 }