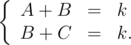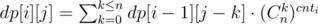Codeforces #144 (Div. 1) B. Table (组合数学+dp)
题目链接:
B.Table
题意:
\(n*m\)的矩阵使每个\(n*n\)矩阵里面准确包含\(k\)个点,问你有多少种放法。
\((1 ≤ n ≤ 100; n ≤ m ≤ 10^{18}; 0 ≤ k ≤ n^2)\)
题解:
- Let \(s_i\) number of points in the column \(i\).
- Two neighboring squares are drawn at this picture, \(A\) is the number of point it the left area (it is one column), \(B\) is the number of points in the middle area and \(C\) is the number of points in the right area (it is one column too). That's why by definition we ###have:
- Therefore \(A = C\).
- That's why 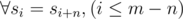
- Divide all columns by equivalence classes on the basis of \(i \mod n\) . For all \(a\) and \(b\) from one class \(s_a = s_b\).
cnta is number of columns in class with 
- There are \(C(n,k)^{cnt_a}\) ways to draw \(k\) points in the each of columns in the class \(a\) independendently of the other classes.
- \(dp[i][j]\) is number of ways to fill all columns in classes \(1, ... i\) in such way that .
- \(cnt_i\) take only two values  and
and 
. Let's calc \(C(n,a)^{cnt_i}\) for all \(a\) and \(cnt_i\) and use it to calc our dp. We have \(O(n^2·k)\) complexity.
代码:
#include<bits/stdc++.h>
#pragma GCC optimize ("O3")
using namespace std;
typedef long long ll;
const int mod = 1e9+7;
using namespace std;
const int N = 123;
const int K = 10000+1230;
ll pow1[N],pow2[N];
ll dp[N][K];
ll c[N][N];
//n*m的矩阵使每个n*n矩阵里面准确包含k个点,问你有多少种放法。
ll quick_pow(ll a,ll b)
{
ll tmp=a;
ll ans=1;
while(b)
{
if(b&1) ans=(ans*tmp)%mod;
tmp=(tmp*tmp)%mod;
b>>=1;
}
return ans;
}
int main()
{
int n,k;
ll m;
cin>>n>>m>>k;
for(int i=0;i<=n;i++) c[i][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
for(int i=0;i<=n;i++)
{
pow1[i]=quick_pow(c[n][i],m/n);
pow2[i]=(pow1[i]*c[n][i])%mod;
}
dp[0][0]=1;
ll now;
for(int i=0;i<n;i++)
{
for(int j=0;j<=k;j++)
{
if(dp[i][j]!=0)
{
for(int p = 0;p <= n && j + p <= k;p++)
{
if(i<m%n) now=pow2[p];
else now=pow1[p];
dp[i+1][j+p]=(dp[i+1][j+p]+dp[i][j]*now)%mod;
}
}
}
}
cout<<dp[n][k]<<endl;
return 0;
}
Codeforces #144 (Div. 1) B. Table (组合数学+dp)的更多相关文章
- Codeforces Round #345 (Div. 1) C. Table Compression dp+并查集
题目链接: http://codeforces.com/problemset/problem/650/C C. Table Compression time limit per test4 secon ...
- Codeforces Round #144 (Div. 2) D table
CodeForces - 233D 题目大意给你一个n*m 的矩阵,要求你进行涂色,保证每个n*n的矩阵内都有k个点被涂色. 问你一共有多少种涂色方案. n<=100 && m& ...
- Codeforces Gym 100338H High Speed Trains 组合数学+dp+高精度
原题链接:http://codeforces.com/gym/100338/attachments/download/2136/20062007-winter-petrozavodsk-camp-an ...
- codeforces 869C The Intriguing Obsession【组合数学+dp+第二类斯特林公式】
C. The Intriguing Obsession time limit per test 1 second memory limit per test 256 megabytes input s ...
- 贪心 Codeforces Round #273 (Div. 2) C. Table Decorations
题目传送门 /* 贪心:排序后,当a[3] > 2 * (a[1] + a[2]), 可以最多的2个,其他的都是1个,ggr,ggb, ggr... ans = a[1] + a[2]; 或先2 ...
- Codeforces #345 Div.1
Codeforces #345 Div.1 打CF有助于提高做题的正确率. Watchmen 题目描述:求欧拉距离等于曼哈顿距离的点对个数. solution 签到题,其实就是求有多少对点在同一行或同 ...
- [CodeForces - 1272D] Remove One Element 【线性dp】
[CodeForces - 1272D] Remove One Element [线性dp] 标签:题解 codeforces题解 dp 线性dp 题目描述 Time limit 2000 ms Me ...
- 让div中的table居中
div 标签上写 style="text-align:center" div中的table中写 style="margin:auto;" <table ...
- Codeforces 219D. Choosing Capital for Treeland (树dp)
题目链接:http://codeforces.com/contest/219/problem/D 树dp //#pragma comment(linker, "/STACK:10240000 ...
随机推荐
- 【Henu ACM Round#15 A】 A and B and Chess
[链接] 我是链接,点我呀:) [题意] 在这里输入题意 [题解] 统计大写和小写的个数. 比较答案.输出即可. [代码] #include <bits/stdc++.h> using n ...
- 解决spring-boot启动中碰到的问题:Cannot determine embedded database driver class for database type NONE(转)
问题 如下: 2017-07-16 08:50:57.436 INFO 13524 --- [ main] c.p.p.web.PointshopWebApplication ...
- 数据库范式小结 1NF 2NF BCNF 3NF 4NF DB normal form
1. 1NF指关系中的每个变量不可再分 2. 2NF指消除了非主属性对码(candidate key)的部分依赖的1NF 比如(S#,C#)-> SN ,(S#,C#)-> SD .S#- ...
- Ajax核心对象——高速上手XmlHttpRequest
引言: 非TGB的.直接跳过吧-- 从开学结束JQuery之后,计算机的进度停了一段时间.某天无聊的时候,又又一次把BS的东西拿过来看了看. 发现里面有非常多既熟悉又陌生的东西. 在学习王兴魁老师的A ...
- js---14公有私有成员方法
var ns1 = {}; //命名空间 ns1.ns11 = {};//子命名空间 ns1.module1 = {name:"a",m:function(){}}; consol ...
- Excel显示当前日期
https://zhidao.baidu.com/question/431460329693825764.html 直接选中单元格,在公示栏输入=now()
- storm单机运行与集群运行问题
使用trident接口时,storm读取kafka数据会将kafka消费记录保存起来,将消费记录的位置保存在tridentTopology.newStream()的第一个参数里, 如果设置成从头开始消 ...
- centos6.5 数据库的安装
mongo https://www.cnblogs.com/layezi/p/7290082.html
- Android-Volley网络通信框架(二次封装数据请求和图片请求(包含处理请求队列和图片缓存))
1.回想 上篇 使用 Volley 的 JsonObjectRequest 和 ImageLoader 写了 电影列表的样例 2.重点 (1)封装Volley 内部 请求 类(请求队列,数据请求,图片 ...
- 探索Oracle之数据库升级八 12c Downgrade 11gR2
探索Oracle之数据库升级八 12c Downgrade 11gR2 前言: 我们前面已经完毕了11gR2 upgrade to 12c 的升级,整个过程还是比較顺利的,尽管和曾经版本号升级有些不太 ...