状态压缩dp初学__$Corn Fields$

明天计划上是要刷状压，但是作为现在还不会状压的\(ruoruo\)来说是一件非常苦逼的事情，所以提前学了一下状压\(dp\)。

鸣谢\(hmq\ juju\)的友情帮助

状态压缩动态规划

本博文的大体内容说明

因为刚学习状态压缩，并且刚做完一道例题。写博客的主要目的是怕自己忘掉，免得以后再重新学习一遍。而那些来踩我博客的同志们，希望以辩证的眼光来看待这篇博文。

于是这篇博客就讲\(Corn Fields\)这一道例题。所以阅读以下内容之前请先浏览一下题目。

基本原理

状态压缩\(dp\)主要是在二进制上进行状态转移的一种动态规划，因为每一个十进制的数可以表示成二进制，所以我们每一行的状态用一个十进制的数来储存。

状态压缩\(dp\)的主要工具

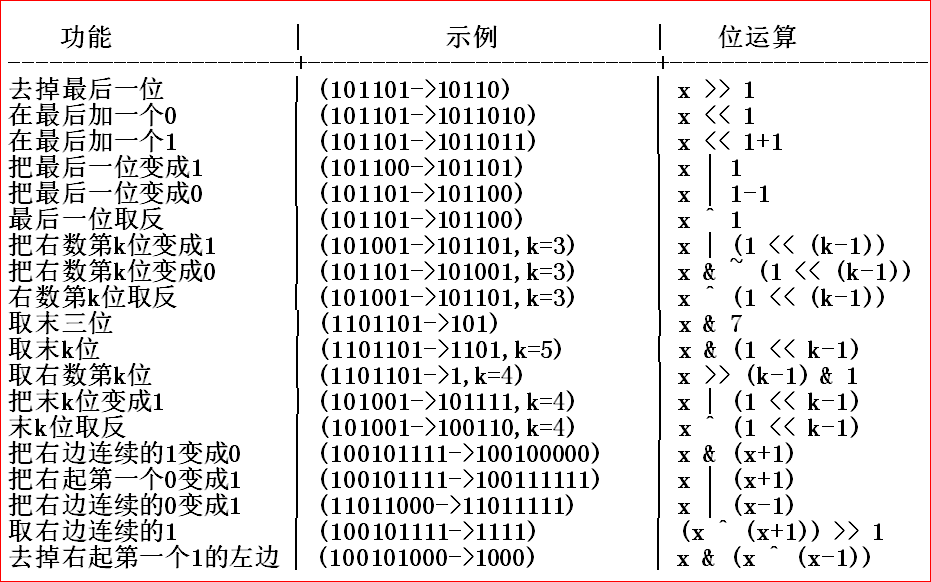
因为状态是在二进制上进行转移的，所以我们需要用到一些位运算来帮助我们进行状态转移。

• |符号，表示或运算，0|1=1,1|1=1,1|0=1,0|0=0。
• &符号，表示与运算，0&1=0,1&1=1,1&0=0,0&0=0。
• ^{符号，表示异或运算，0}1=1,1^1=0,10=1,0^0=0。
• <<符号，表示在2进制下小数点向右移动若干位，1<<2=4,3<<1=6。
• >>符号，表示在2进制下小数点向左移动若干位，2>>1=1,13>>3=1。
• 判断数字x第i位是否是1——if (x&(1<<i))。
• 将一个数字x第i位改变为1——x|=(1<<i)。

状态压缩\(dp\)实现的基本过程

1. 首先枚举所有的情况。根据题意，\(1\)表示有草，\(0\)表示没草，然后又有\(n\)位，所以我们就枚举\(0\sim2^n\)的位数，为啥尼?
   
   因为\(0\)表示没有草的情况，而\(2^n\)也就是\(\begin{matrix} \underbrace{ 1\cdots1 } \\ n\end{matrix}\)这种全是草的情况，所以要这样枚举。然后我们在存储合法状态，存到\(state\)数组里。
2. 枚举完之后，我们的所有情况出来了，我们要进行存图，存图也要用二进制。这里我们存图用一个\(cur\)数组，这个数组表示图的存储，为了方便，我们将无草转变为\(1\)，有草为\(0\)。
3. 然后就是进行状态存储。我们已经有了合法状态，我们也有图，我们就要枚举判断合法状态内的可行状态。
   
   这里我们要用到一个\(fit\)函数。fit函数可以帮助我们判断合不合理，然后找到可行状态
4. 状态转移。设\(dp[i][j]\)表示第\(i\)行的第\(j\)个状态。
   
   状态转移要枚举上一层的状态。然后方程很简单\(dp[i][j]=dp[i][j]+dp[i-1][k]\)。

例题代码讲解

首先我们看一下如何枚举状态

inline void init()//初始化
{
    int sum=1<<n,i;//列举可能状态，并预存
    for (i=0;i<sum;i++)
        if (!(i&(i<<1)))//枚举合法状态
            state[++tot]=i;
}

为什么\(!(i\&(i<<1))\)呢，因为你只要有牧草重叠，这个数绝对不会为\(0\)。

然后看一下图的存储

    for (i=1;i<=m;i++)
        for (j=1;j<=n;j++)
        {
            k=read();
            if (!k)
                cur[i]+=(1<<(n-j));
        }

为啥是左移\(n-j\)为呢\(?\)

因为你是从右往左来储存二进制的，第\(j\)位如果反过来肯定是第\(n-j\)位咯。

\(fit\)函数

inline bool fit(int x,int k)//判断当前状态是否符合当前行
{
    return !(state[x]&cur[k]);
}

只要这一个函数理解了，状压就基本搞定了。

因为\(state\)存储的是合法状态，\(cur\)存储的是不合法状态，所以两者按位与，合法状态的数一定为\(0\)，不合法状态的数一定不为\(0\)。这里有的同志就开始疑惑了，为啥尼？

你想想\(state\)里面\(1\)为有草，\(cur\)里面\(1\)为无草，而\(1\&1\)则代表有值，那么这个方案可行吗？

就这样我们能进行第一行的初始化咯

    for (i=1;i<=tot;i++)//初始化第一行
        if (fit(i,1))
            dp[1][i]=1;

状态转移

状态转移相对来说就比较简单了。

    for (i=2;i<=m;i++)//枚举行
        for (j=1;j<=tot;j++)//枚举当前状态
        {
            if (!fit(j,i))//如果这一层的方案不在可行方案里
                continue;
            for (k=1;k<=tot;k++)//枚举上一层可行状态
            {
                if (!fit(k,i-1))//如果这一层的方案不在可行方案里
                    continue;
                if (state[j]&state[k])//如果上一层的可行方案与这一层可行方案冲突，意思是上下有草挨着
                    continue;
                dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;//状态转移
            }
        }

具体可能的疑问都在代码中注释了

第一层枚举行数，第二层枚举可行方案，第三层枚举上一层的可行方案，万事大吉！

代码

#include<cstdio>
#include<iostream>
#include<cctype>
#define mod 100000000
#define C continue//懒得打hhhhh
using namespace std;
int n,m,tot,state[1500],dp[15][1500],ans,cur[15];//dp表示当前最大值，第一维是行数，第二维是状态数，cur是每行的情况，state是预存的可能状态
inline int read()//读入优化
{
    int x=0,f=1;
    char c=getchar();
    while (!isdigit(c))
        f=c=='-'?-1:1,c=getchar();
    while (isdigit(c))
        x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return x*f;
}

inline bool fit(int x,int k)//判断当前状态是否符合当前行
{
    return !(state[x]&cur[k]);
}

inline void init()//初始化
{
    int sum=1<<n,i;//列举可能状态，并预存
    for (i=0;i<sum;i++)
        if (!(i&(i<<1)))//枚举合法状态
            state[++tot]=i;
}
int main()
{
    int i,j,k;
    m=read();
    n=read();
    init();
    for (i=1;i<=m;i++)
        for (j=1;j<=n;j++)
        {
            k=read();
            if (!k)
                cur[i]+=(1<<(n-j));
        }
    for (i=1;i<=tot;i++)//初始化第一行
        if (fit(i,1))
            dp[1][i]=1;
    for (i=2;i<=m;i++)//枚举行
        for (j=1;j<=tot;j++)//枚举当前状态
        {
            if (!fit(j,i))//如果这一层的方案不在可行方案里
                continue;
            for (k=1;k<=tot;k++)//枚举上一层可行状态
            {
                if (!fit(k,i-1))//如果这一层的方案不在可行方案里
                    continue;
                if (state[j]&state[k])//如果上一层的可行方案与这一层可行方案冲突，意思是上下有草挨着
                    continue;
                dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;//状态转移
            }
        }
    for (i=1;i<=tot;i++)
        ans=(ans+dp[m][i])%mod;
    printf("%d",ans);
    return 0;
}