洛谷1387 二维dp 不是特别简略的题解 智商题

#洛谷1387
dp题目，刚开始写的时候使用了前缀和加搜索，复杂度大概在O(n ^ 3)级别，感觉这么写还是比较对得起*普及/提高-*的难度的。。后来看了题解区各位大神的题解，开始一脸mb，之后备受启发。

设dp[i][j]表示以(i, j)为右下点的正方形的最大边长，则转移方程如下：

dp[i][j] = min{dp[i-1][j], dp[i][j-1], dp[i-1][j-1]} + 1 (a[i][j] == 1)

dp[i][j] = 0 (a[i][j] == 0)

转移非常简单，但是正确性却不是那么显然，考虑对于一个以(i,j)为右下点的正方形，



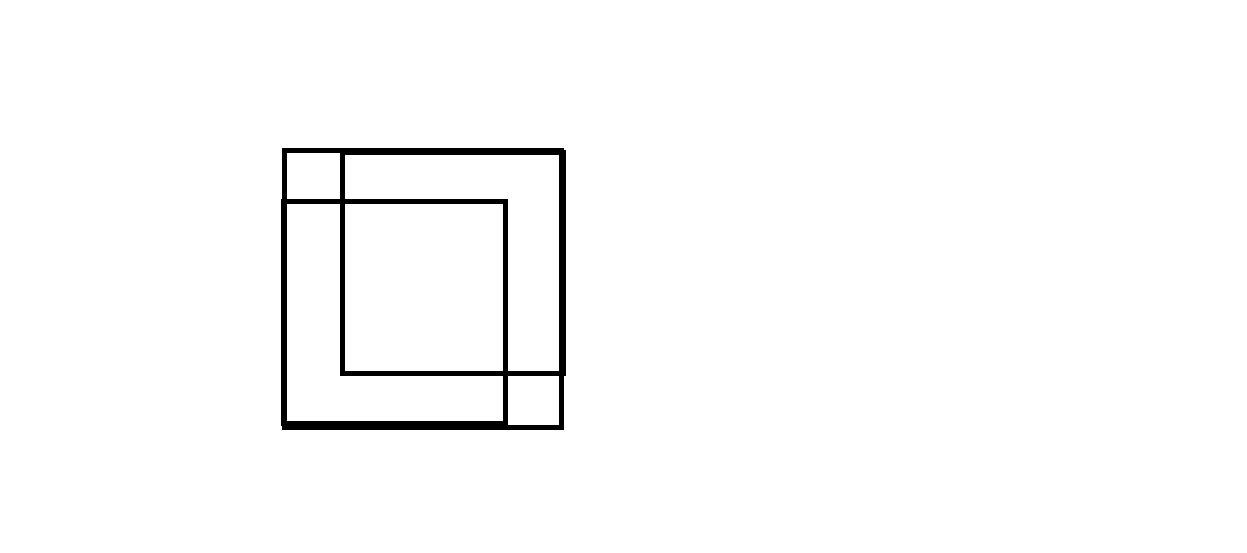
它正是由dp[i-1][j],dp[i][j-1],dp[i-1][j-1]三个正方形来限制，所以该正方形一定会满足三个正方形中最小的，可证明合法性

又可以发现，如果此时考虑的正方形边长超过了min() + 1，那么一定会与三正方形中最小的冲突，可证明最优性。

由此可推得方程

#include <cstdio>
#include <cstring>
#include <algorithm>

const int maxn = 100 + 10;

int a[maxn][maxn];
int dp[maxn][maxn];
int n, m;

int main () {
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++) scanf("%d", &a[i][j]);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++) {
			if (a[i][j] == 0) continue;
			dp[i][j] = std :: min(dp[i-1][j], dp[i][j-1]);
			dp[i][j] = std :: min(dp[i][j], dp[i-1][j-1]);
			dp[i][j]++;
		}
	int ans = 0;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			if (ans < dp[i][j]) ans = dp[i][j];
	printf("%d", ans);
	return 0;
}