ABC267G Increasing K Times 题解

做这道题，很有感悟，发篇文。

先给数列从小到大排个序。

接下来设 \(f_{i,j}\) 表示前 \(i\) 个数的排列形成 \(j\) 个上坡的方案数。

接下来考虑转移，分为插入第 \(i\) 个数后增加上坡和不增加上坡两种情况。

对于不增加的情况，有三种可能：

• 第 \(i\) 个数插入在了数列的最前端，有 \(1\) 种方案。
• 第 \(i\) 个数插入在了一个上坡的中间，因为上坡中较小的那个数字必定小于第 \(i\) 个数，形成一个上坡，较大的那个数字必定小于等于第 \(i\) 个数，不形成上坡，而我们拆散了一个上坡，故没有增加，有 \(j\) 种方案。
• 第 \(i\) 个数插入在了数值相同的数后面，这个记为 \(same_i\)，有 \(same_i\) 种方案。

对于增加的情况，就是减去这三种情况了，不过增加了，就说明原来只有 \(j-1\) 个上坡，这里和上面不太一样。

整理式子，得：

\[f_{i,j} = f_{i-1,j-1} \times (i - j - same_i) + f_{i-1,j} \times (1 + j + same_i)
\]

这样就可以 \(O(n^2)\) 求得了,可以用滚动数组。

#include <bits/stdc++.h>
using namespace std;
long long n, k, a[5005], f[5005], same[5005], sum;
int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a + 1, a + n + 1);
    for (int i = 1; i <= n; i++) {
        if (a[i] == a[i - 1])
            same[i] = same[i - 1] + 1;
    }
    f[0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = i - same[i]; j >= 1; j--) {
            f[j] = f[j - 1] * (i - j - same[i]) % 998244353 + f[j] * (1 + j + same[i]) % 998244353;
            f[j] %= 998244353;
        }
        f[0] = f[0] * (1 + same[i]) % 998244353;
    }
    cout << f[k] << endl;
}

After Increasing K Times

过了一段时间重新看了一下这道题，发现有几个优化，也顺便介绍一下。

首先，我们发现 \(n\) 很大，但是数值区间很小，所以考虑使用桶排序，因为数字在 \([1,n]\),所以排序复杂度为 \(O(n)\)。

然后，我们发现枚举区间可以缩小，因为我们并不是全都需要，简单用一个图表示：

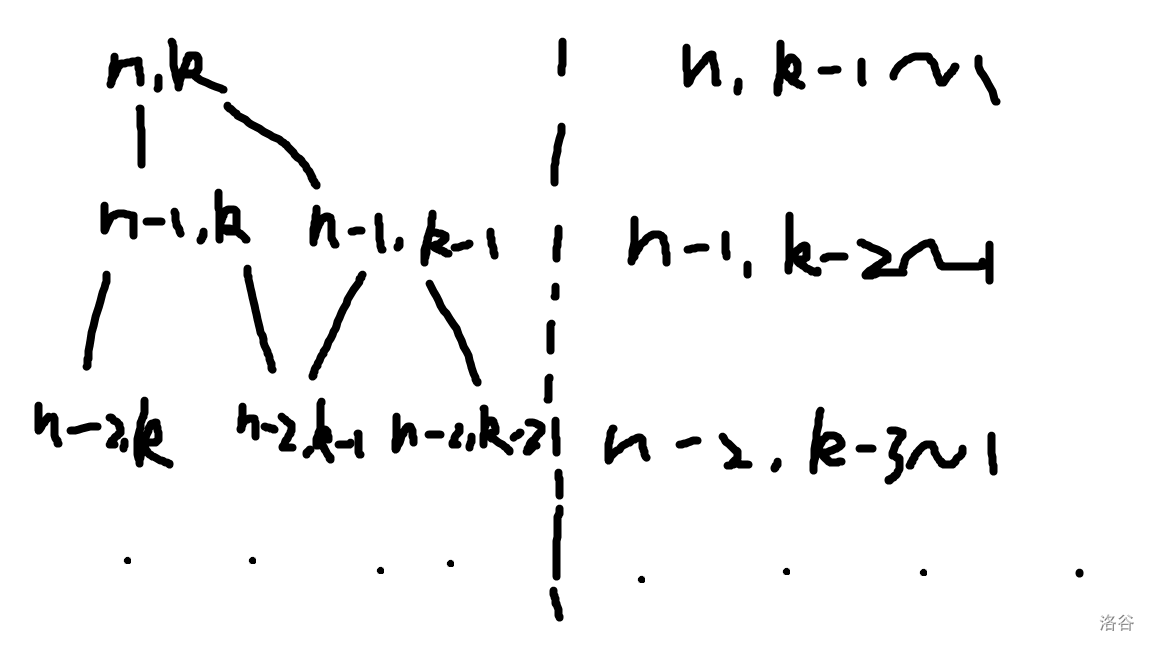
左边是我们需要的值，右边是不需要的。

那么，有用的状态的区间边界很好推算，是 \([k+n-i+1,k]\)，这个优化可以减少接近一半的时间。

以上优化让代码大大提速，获得了洛谷最优解，在 AtCoder 排名第二（截至2022.11.23）。

第一名本人丧心病狂卡常也卡不过，快了 4ms，但是本代码很短，最快代码使用了 IDFT。

#include <stdio.h>
inline int read() {
    char c = getchar();
    int sum = 0;
    while (c < '0' || c > '9') c = getchar();
    do {
        sum = (sum << 3) + (sum << 1) + c - '0';
        c = getchar();
    } while (c >= '0' && c <= '9');
    return sum ;
}
int n, k,s[5005],b[5005],t=1;
long long f[5005];
int main() {
    n=read(),k=read();
    for (int i = 1; i <= n; i++)b[read()]++;
    for(int i=1;i<=n&&t<=n;i++)
    {
    	if(b[i])b[i]--,t++;
    	while(b[i])b[i]--,s[t] = s[t - 1] + 1,t++;
	}
    f[0] = 1;
    for (int i = 1; i <= n; i++) {
		int r=(k>i-s[i])?(i-s[i]):k,l=(k-n+i-1>1)?(k-n+i-1):1;
        for (int j = r; j >= l; j--) {
            f[j] = f[j] * (j + s[i] + 1) + f[j - 1] * (i - j - s[i]) ;
            f[j] %= 998244353;
        }
        f[0] = f[0] * (s[i] + 1) % 998244353;
    }
    printf("%lld\n",f[k]);
    return 0;
}