（stm32f103学习总结）—GPIO结构

一、GPIO基本结构

二、GPIO工作模式

输入模式

输入浮空

输入上拉

输入下拉

模拟输入

输出模式

开漏输出

开漏复用功能

推挽式输出

推挽式复用功能

库函数中所对应的代码

 1 typedef enum
 2 { 
 3 　　GPIO_Mode_AIN = 0x0, /* 模拟输入 */
 4    GPIO_Mode_IN_FLOATING = 0x04, /* 浮空输入，复位后的状态 */
 5    GPIO_Mode_IPD = 0x28, /* 下拉输入，这里的下拉是指单片机内部的电阻 */
 6    GPIO_Mode_IPU = 0x48, /* 上拉输入，这里的上拉是指单片机内部的电阻 */
 7    GPIO_Mode_Out_OD = 0x14, /* 开漏输出 */
 8    GPIO_Mode_Out_PP = 0x10, /* 推挽输出 */
 9    GPIO_Mode_AF_OD = 0x1C, /* 复用开漏输出 */
 10   GPIO_Mode_AF_PP = 0x18 /* 复用推挽输出 */
11 }GPIOMode_TypeDef;

GPIO的工作模式有这么多那么每个模式是怎样工作的呢？下面以图片的形式进行讲解

那么先来讲解输入模式下的4种工作方式（输入浮空、输入上拉、输入下拉、模拟输入）

（1）输入浮空模式

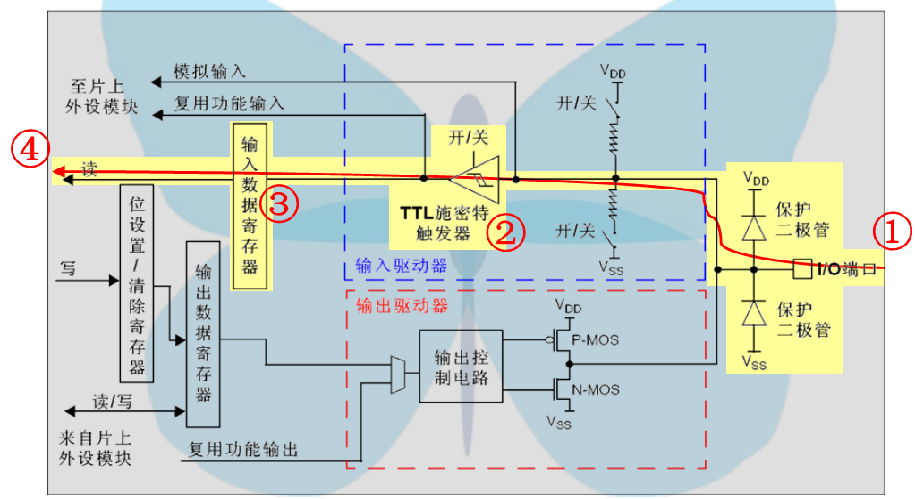
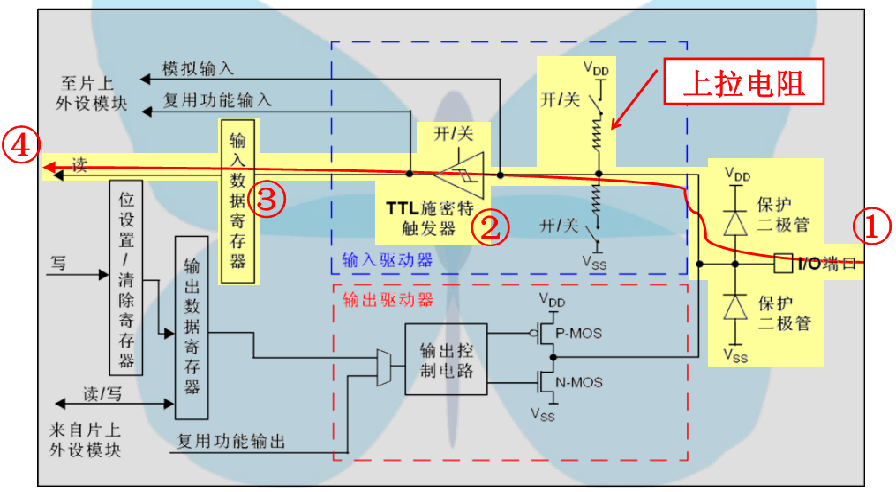
（2）输入上拉模式

（3） 输入下拉模式

（4）模拟输入模式

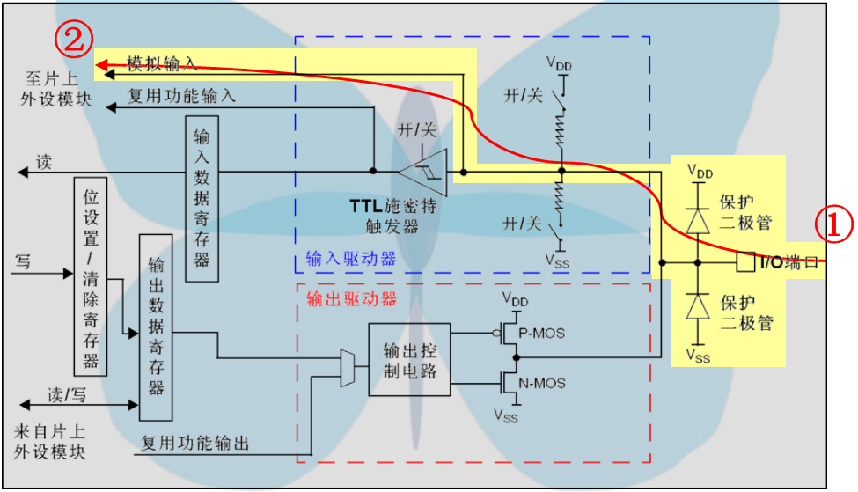
上面的几种输入模式根据图所示的路线应该很好理解，悬空输入就是你输入进来的啥我就接受啥，输入上拉就是你不输入的时候我就是高电平，输入下拉与输入上拉情况相反，模拟输入的话就是用来接受模拟量（电压值），一般用于AD采集。

看完输入的几种模式后接下来学习下GPIO输出的几种工作模式

（1）开漏输出模式

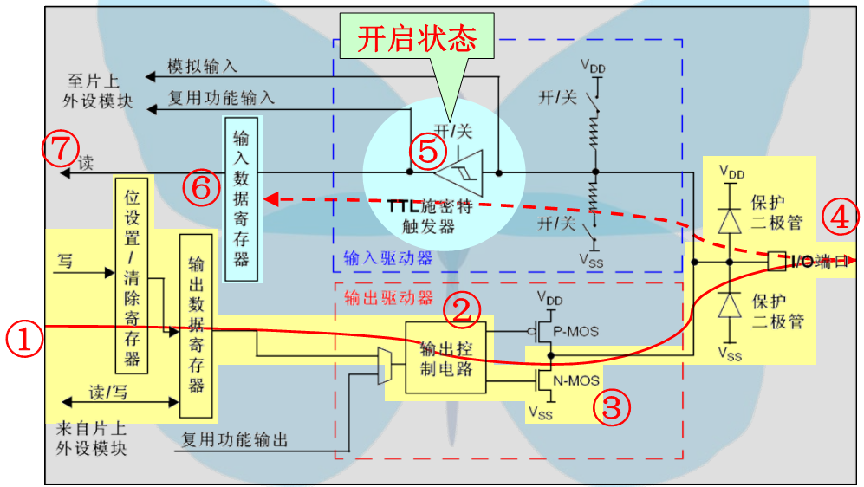
（2）开漏复用输出模式

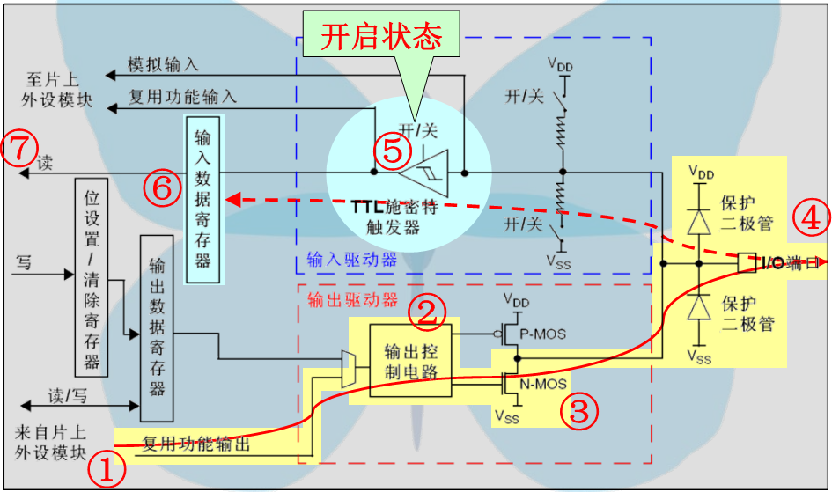
　　开漏形式输出端相当于三极管的集电极，要得到高电平状态需要上拉电阻才行。开漏形式的电路有以下几个特点：

1、利用外部电路的驱动能力，减少IC内部的驱动。当IC内部MOSFET导通时，驱动电流是从外部的VCC流经上拉电阻、MOSFET到GND。IC内部仅需很小的栅极驱动电流。

2、一般来说，开漏是用来连接不同电平的器件，匹配电平用的，因为开漏引脚不连接外部的上拉电阻时，只能输出低电平，如果需要同时具备输出高电平的功能，则需要接上拉电阻，很好的一个优点是通过改变上拉电源的电压，便可以改变传输电平。比如加上上拉电阻就可以提供TTL/CMOS电平输出等。（上拉电阻的阻值决定了逻辑电平转换的速度。阻值越大，速度越低功耗越小，所以负载电阻的选择要兼顾功耗和速度。）

3、开漏输出提供了灵活的输出方式，但是也有其弱点，就是带来上升沿的延时。因为上升沿是通过外接上拉无源电阻对负载充电，所以当电阻选择小时延时就小，但功耗大；反之延时大功耗小。所以如果对延时有要求，则建议用下降沿输出。

4、可以将多个开漏输出连接到一条线上。通过一只上拉电阻，在不增加任何器件的情况下，形成"与逻辑"关系，即"线与"。可以简单的理解为：在所有引脚连在一起时，外接一上拉电阻，如果有一个引脚输出为逻辑0，相当于接地，与之并联的回路"相当于被一根导线短路"，所以外电路逻辑电平便为0，只有都为高电平时，与的结果才为逻辑1。

开漏输出就是不输出电压，低电平时接地，高电平时不接地。如果外接上拉电阻，则在输出高电平时电压会拉到上拉电阻的电源电压。这种方式适合在连接的外设电压比单片机电压低的时候。输出端出跟集电极开路十分相似，工作原理也是一样的。不同的是，开漏输出使用的场效应管，使用时要加上拉电阻。（挺绕的，有机会用具体工程来介绍）

（3）推挽输出模式

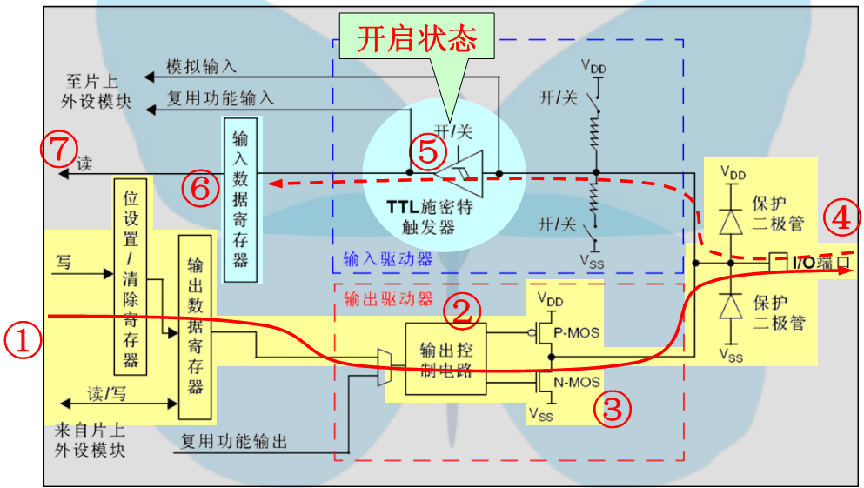
（4）推挽复用输出模式

　　推挽输出可以输出高、低电平，连接数字器件；推挽结构一般是指两个三极管分别受两个互补信号的控制，总是在一个三极管导通的时候另一个截止。高低电平由IC的电源决定。

　　推挽电路是两个参数相同的三极管或MOSFET，以推挽方式存在于电路中，各负责正负半周的波形放大任务，电路工作时，两只对称的功率开关管每次只有一个导通，所以导通损耗小、效率高。输出既可以向负载灌电流，也可以从负载抽取电流。推拉式输出级既提高电路的负载能力，又提高开关速度。

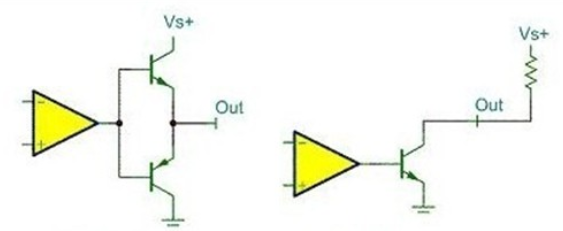
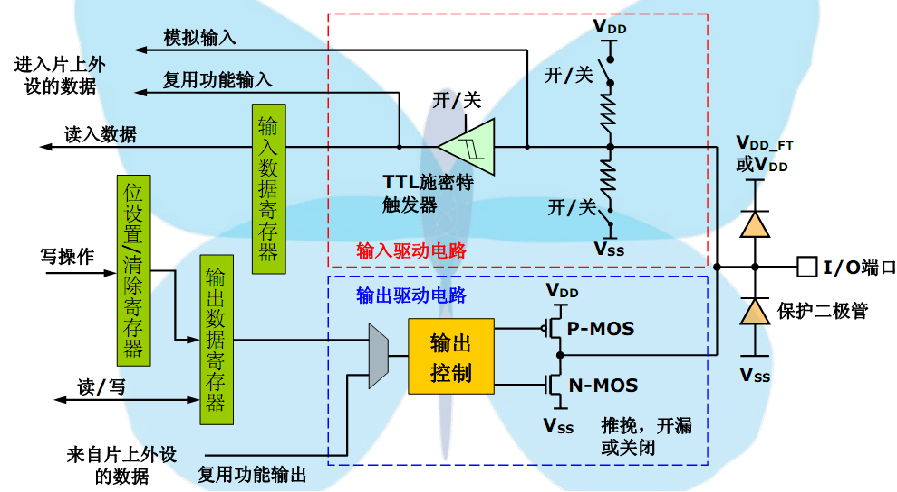
　　关于推挽输出和开漏输出，用一幅最简单的图形来概括：该图中左边的便是推挽输出模式，其中比较器输出高电平时下面的PNP三极管截止，而上面NPN三极管导通，输出电平VS+；当比较器输出低电平时则恰恰相反，PNP三极管导通，输出和地相连，为低电平。右边的则可以理解为开漏输出形式，需要接上拉。

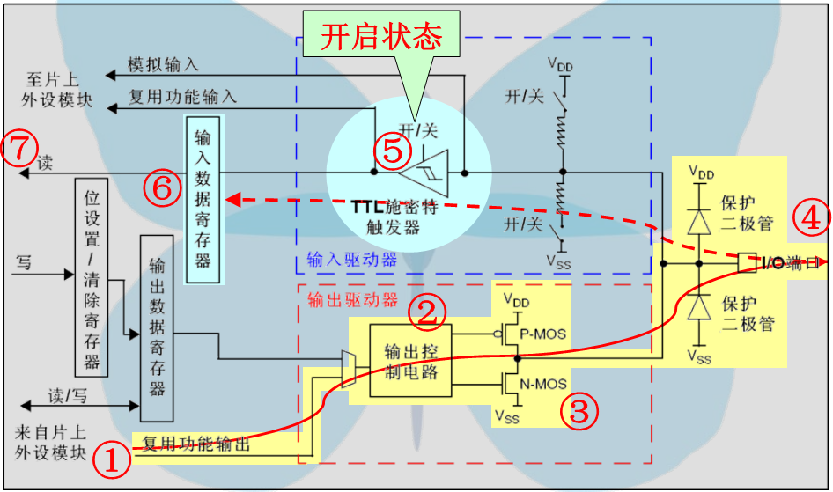
复用开漏 / 推挽输出

可以认为是GPIO口被用作第二功能时的配置情况（即并非作为通用IO口使用），开漏 / 推挽输出

下图是截取的stm32f103中I/O口对应的功能PA1除了当做普通I/O之外还有USART2、ADC、TIM5、TIM2的功能

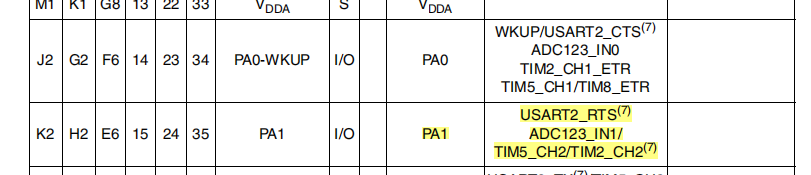
　　其实到这关于GPIO的这几个工作模式就已经说完了，但是各位是否心中有个疑问，为什么输入里面没有说复用输入呢？（输出模式可是有复用输出的相关模式的）

　　我们再来看看GPIO的结构图，红色的框内和蓝色的框内是不是有一个很大的不同，蓝色的框内有个梯形的东西（这个是用来选择哪个输出的）而输入这边没有，所以在输入的时候模拟输入、复用功能对应的片上外设、以及读入数据对应CPU都可以去读取I/O寄存器或者相应寄存器的值（都是从I/O口一个个输入进去的），前提是你打开相应的片上外设时钟且使能，比如说复用功能需要输入的数据那么对应的这个片上外设就应该使能且时钟也使能，这个外设就可以通过读自己的数据寄存器的值来得到I/O口的数据了（这寄存器和读入数据中的输入数据寄存器原理上是一样的）