omc.

OMC 099(4b) D

因为 \((abc)^{\dfrac 13} \le \dfrac{a+b+c}3\)（基本不等式），将 \(a = xy, b = yz, c = xz\) 代入得到 \((xyz)^{\dfrac 23} \le \dfrac{xy+yz+xz}3 = \langle 2,2,4 \rangle\)，所以 \(xyz \le \langle 3,3,6 \rangle\)，于是 \(\dfrac1x+\dfrac1y+\dfrac1z = \dfrac{xy+yz+xz}{xyz} \ge \dfrac{\langle2,3,4\rangle}{\langle3,3,6\rangle} = \dfrac{1}{\langle 1,0,2\rangle} = \dfrac1{\bf 50}\)，根据题目要求，显然可以取等号。

OMC 095(4b) D

令 \(y = x - 11\)，则 \(y \equiv 0 \pmod{10/9/8/7/6}\)，也就是 \(y \equiv 0 \pmod{\mathrm{lcm}(6, 7, 8, 9, 10)}\)，所以 \(x \equiv 11 \pmod{\mathrm{lcm}(6, 7, 8, 9, 10)}\)，经过计算 \(\mathrm{lcm}(6, 7, 8, 9, 10) = 2520\)，\(x = \lfloor\dfrac{10^4 - 1 - 11}{2520}\rfloor \times 2520 + 11 = \bf 7571\)。

OMC 093(4b) C

定理：圆的外切四边形的两组对边的和相等。

于是 \(\rm AD+BC = 55+89 = 144\)，所以根据基本不等式， \(\rm (AD \times BC)^{\dfrac 12} \le \dfrac{(AD+BC)}2\)，于是 \(\rm (AD \times BC) \le (\dfrac{AD+BC}2)^2 = 72^2 = \bf 5184\)。

OMC 090(4b) C

对于一个等差数列 \(a_1, a_2, \dots, a_{100}\)，有 \(a_{100} - a_1 = 99 \times d\)，这里 \(d\) 即为公差（\(a_2 - a_1\)），于是我们只需要找 \(99 \mid (a_{100} - a_1)\)，或者说，\(a_1 \equiv a_{100} \pmod{99}\)。特殊地，\(10^4\) 以下有 \(102\) 个 \(\equiv 1 \pmod{99}\) 的，\(\not\equiv 1 \pmod{99}\) 只有 \(101\) 个，于是答案为 \(\mathrm C_{102}^2 + \mathrm C_{101}^2 \times 98 = \bf 500051\)。

OMC 080(4b) B

使用解析几何解题。

设圆的半径为 \(r\)，则 \(\rm A,B,C,P\) 的坐标可以如下图表示：

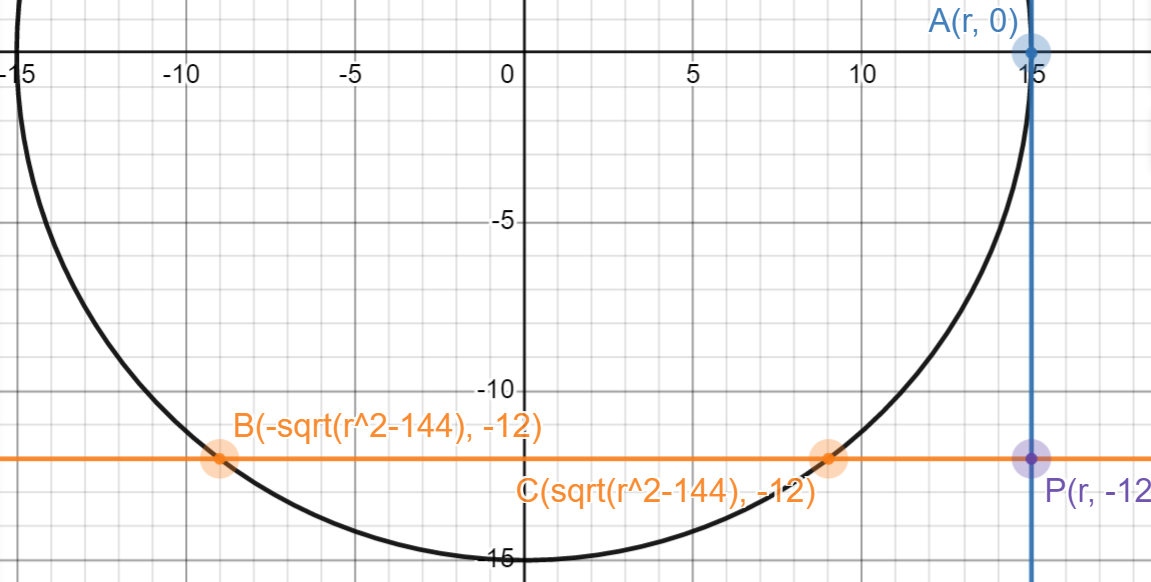
于是 \(y_{\rm B}=y_{\rm P}\)，\({\rm BP} = r+\sqrt{r^2-12^2} = 6\)，解方程可得 \(r = {\bf 15}\)。

OMC 076(4b) B

首先考虑最高名次，于是做对 C 题的人最多只能得到 300 分（尽可能），于是设置 3 个 300 分选手，剩下 7 个选手，最多也只有 300 分了，于是分数排列为 300,300,300,300,300,300,300,300,300,100,100。

又因为 300 也有可能比选手高，所以也设置 3 个 300 分选手，不浪费 AB 名额，而 B 题选手必须和 A 一起都做对才能超越那个人，分数排列同上。

由于选手会在 \(300\) 分的 \(1 \sim 8\) 名都可能，所以答案为 \(\dfrac{(8+1)8}{2} = \bf 36\)。

OMC 111(4b) B

因为 \(S(x) \equiv x \pmod 9\)，所以 \(x\) 满足性质的必要条件是 \(x^2 \equiv (x+1)^2 \pmod 9\)，或者说 \(x \equiv 4 \pmod 9\)，将 \(4,13,22,31,40,49\) 一起带入公式得到 \(4+13+22+49 = \bf 88\)。

OMC 111(4b) C

组合数学好题。

显然可以转化为求一个长度为五的单调不降序列，其中每个元素都在 \([0,5]\)，但是序列不能是全 \(0\) 的序列的数量。

设这个序列为 \(a\)，设 \(b_i := a_i + i\)。于是问题转换为严格单调递增序列，其中每个元素都在 \([1,10]\)，但是序列不能是 \(1,2,3,4,5\)。答案显然是 \(10\) 个数任意无序取 \(5\) 个刨除一个 \(1,2,3,4,5\)，答案为 \(\mathcal C_{10}^5-1=\bf 251\)。

OMC 109(4b) D

几何好题。

因为 \(\Delta \rm ABC\) 是等边三角形，所以 \(\angle \rm ABC = \angle CAB = \angle BCA = 60^\circ\)，所以 \(\angle \rm ABP = 60^\circ - 2{\it x},\angle \rm APB = 120^\circ + {\it x}\)（设 \(x = \angle \rm PAB\)），同样计算可得 \(\angle \rm CPB = 120^\circ + {\it x}\)，因为 \({\angle \rm APB = \angle CPB};{\rm AB=BC};{\rm PB=PB};{\rm \angle \rm CPB > 120^\circ > 90^\circ}\)，所以 \(\rm \Delta APB = \Delta CPB\)（\(\rm SSA\) 在钝角情况下可以证明全等）

因为 \(x \ne 3x\)，所以 \(x = 60^\circ - 3x = 15^\circ\)，得到 \(a=4,A=135^\circ,B=15^\circ,C=30^\circ\)，因为 \(\dfrac A{\sin A}=\dfrac B{\sin B} = \dfrac C{\sin C} = \dfrac 4{\sin 135^\circ} = 4\sqrt 2\)，所以 \(b = 4\sqrt 2 \times \sin 30^\circ = 2 \sqrt 2\)，于是 \(S = \dfrac{ab\sin C}2=\dfrac 12 \times \dfrac{\sqrt 3-1}{2\sqrt 2} \times 4 \times {2 \sqrt 2} = \bf{ \sqrt{12} - 2 }\)

\(\Huge{评论区禁止膜拜！}\)