〇、目标

1、使用Weka平台，并在该平台使用数据导入、可视化等基本操作；

2、对K-means算法的不同初始k值进行比较，对比结果得出结论。

一、打开Weka3.8并导入数据

二、导入数据

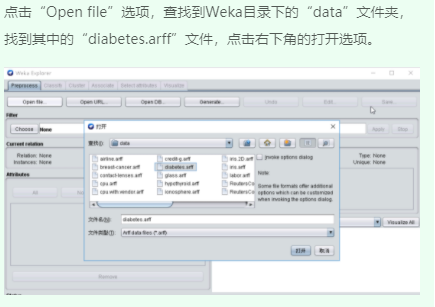
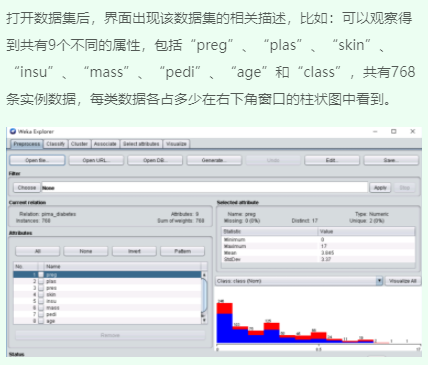
三、SimpleKMeans算法聚类

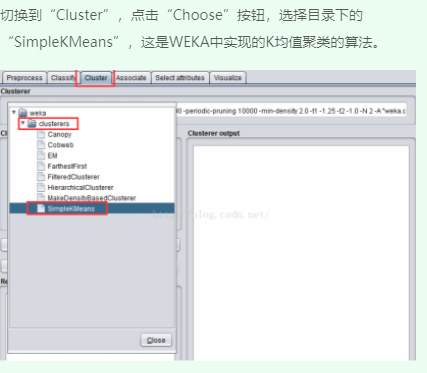
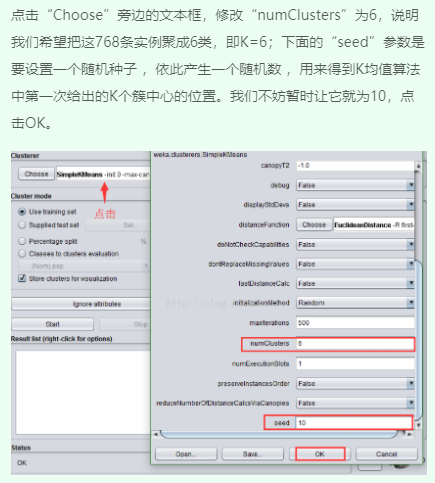
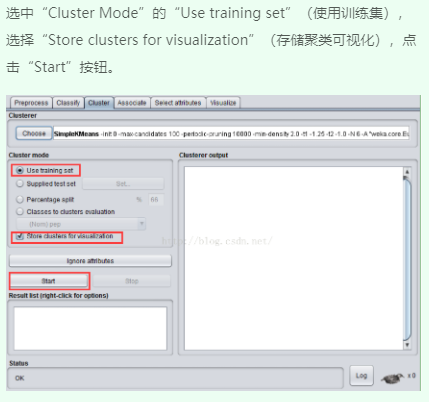
四、运行观察结果

1、观察聚类输出结果

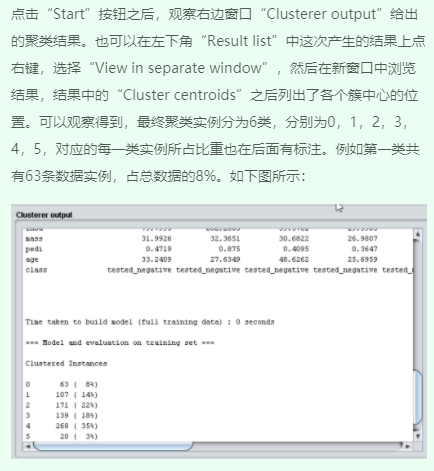
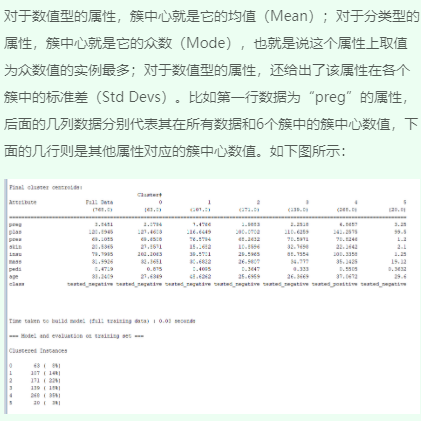
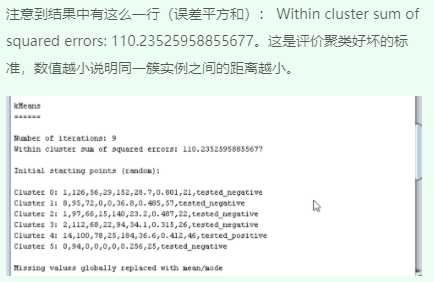
2、修改参数值重新运行并观察结果

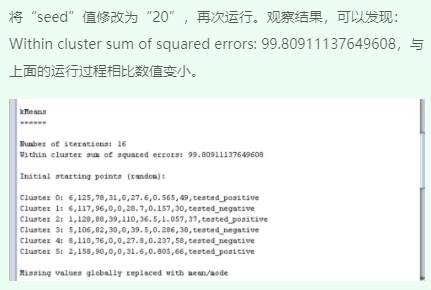
3、可视化聚类结果

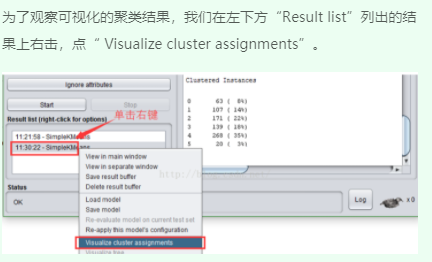
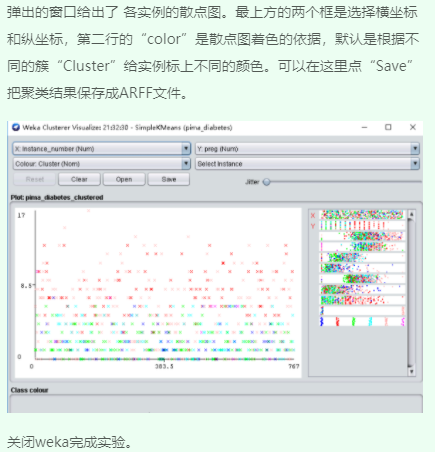
3.7：基于Weka的K-means聚类的算法示例的更多相关文章

  1. R与数据分析旧笔记（十五） 基于有代表性的点的技术：K中心聚类法

    基于有代表性的点的技术:K中心聚类法 基于有代表性的点的技术:K中心聚类法 算法步骤 随机选择k个点作为"中心点" 计算剩余的点到这个k中心点的距离,每个点被分配到最近的中心点组成 ...

  2. 聚类之K均值聚类和EM算法

    这篇博客整理K均值聚类的内容,包括: 1.K均值聚类的原理: 2.初始类中心的选择和类别数K的确定: 3.K均值聚类和EM算法.高斯混合模型的关系. 一.K均值聚类的原理 K均值聚类(K-means) ...

  3. 100天搞定机器学习|day44 k均值聚类数学推导与python实现

    [如何正确使用「K均值聚类」? 1.k均值聚类模型 给定样本,每个样本都是m为特征向量,模型目标是将n个样本分到k个不停的类或簇中,每个样本到其所属类的中心的距离最小,每个样本只能属于一个类.用C表示 ...

  4. 5-Spark高级数据分析-第五章 基于K均值聚类的网络流量异常检测

    据我们所知,有‘已知的已知’,有些事,我们知道我们知道:我们也知道,有 ‘已知的未知’,也就是说,有些事,我们现在知道我们不知道.但是,同样存在‘不知的不知’——有些事,我们不知道我们不知道. 上一章 ...

  5. ML: 聚类算法-K均值聚类

    基于划分方法聚类算法R包: K-均值聚类(K-means)                   stats::kmeans().fpc::kmeansruns() K-中心点聚类(K-Medoids) ...

  6. 【转】算法杂货铺——k均值聚类(K-means)

    k均值聚类(K-means) 4.1.摘要 在前面的文章中,介绍了三种常见的分类算法.分类作为一种监督学习方法,要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别与之对应.但是很多时 ...

  7. 机器学习实战5：k-means聚类：二分k均值聚类+地理位置聚簇实例

    k-均值聚类是非监督学习的一种,输入必须指定聚簇中心个数k.k均值是基于相似度的聚类,为没有标签的一簇实例分为一类. 一 经典的k-均值聚类 思路: 1 随机创建k个质心(k必须指定,二维的很容易确定 ...

  8. SciPy k均值聚类

    章节 SciPy 介绍 SciPy 安装 SciPy 基础功能 SciPy 特殊函数 SciPy k均值聚类 SciPy 常量 SciPy fftpack(傅里叶变换) SciPy 积分 SciPy ...

  9. Sklearn K均值聚类

    ## 版权所有,转帖注明出处 章节 SciKit-Learn 加载数据集 SciKit-Learn 数据集基本信息 SciKit-Learn 使用matplotlib可视化数据 SciKit-Lear ...

  10. Python实现kMeans(k均值聚类)

    Python实现kMeans(k均值聚类) 运行环境 Pyhton3 numpy(科学计算包) matplotlib(画图所需,不画图可不必) 计算过程 st=>start: 开始 e=> ...

随机推荐

  1. kvm上已安装的虚拟机修改为桥接网络

    kvm上安装的虚拟机默认使用的nat网络格式,现在已经调整kvm主机为桥接方式了,但是已经安装的虚拟机还是nat方式,所以需要修改一下 让KVM虚拟主机使用桥接网络br0 修改虚拟机的配置文件,默认存 ...

  2. 第六章：Django 综合篇 - 3：使用MySQL数据库

    在实际生产环境,Django是不可能使用SQLite这种轻量级的基于文件的数据库作为生产数据库.一般较多的会选择MySQL. 下面介绍一下如何在Django中使用MySQL数据库. 一.安装MySQL ...

  3. kubernetes1.20 部署 traefik2.3

    一.概述 Traefik 是一个开源的可以使服务发布变得轻松有趣的边缘路由器.它负责接收你系统的请求,然后使用合适的组件来对这些请求进行处理. 除了众多的功能之外,Traefik 的与众不同之处还在于 ...

  4. PR中导入的照片在画面上只显示一部分的解决办法

    这是因为图片的分辨率太大导致的. 1.图片的分辨率大于PR工程的设置的时候,就会只显示局部. 2.可以用PS把图片先缩小为工程大小即可. 3.也可以把图片拖到时间线上,右键点击,缩放为帧大小即可. 这 ...

  5. DevExpress弹框、右键菜单、Grid的使用

    很重要!!!Dev为了区分winform的命名,会把一些新添加的属性放在Properties对象里!!找不到想要的属性,记得到里面找找哦! 一.下拉框 在这里假设我们的数据源是db.List(),在这 ...

  6. IOC常用的创建对象方式

    通过无参构造方法来创建 1.User.java public class User { private String name; public User() { System.out.println( ...

  7. PHP微信支付功能

    百度网盘:http://pan.baidu.com/s/1sl5GeVr  l5ud 先下载一份sdk ,引入到自己的项目中,我用的是TP5,配置好namespace 然后在项目中引入: 之后,在去配 ...

  8. Vue学习之--------组件在Vue脚手架中的使用（代码实现）（2022/7/24）

    文章目录 1.第一步编写组件 1.1 编写一个 展示学校的组件 1.2 定义一个展示学生的信息组件 2.第二步引入组件 3.制作一个容器 4.使用Vue接管 容器 5.实际效果 6.友情提示: 7.项 ...

  9. Hadoop集群简单入门

    Hadoop集群搭建 自己配置Hadoop的话太过复杂了,因为自己着急学习,就使用了黑马的快照.如果小伙伴们也想的话可以直接看黑马的课程,快照的话关注黑马程序员公众号,输入Hadoop就能获取资料,到 ...

  10. 开源项目在线化 中文繁简体转换/敏感词/拼音/分词/汉字相似度/markdown 目录

    前言 以前在 github 上自己开源了一些项目.碍于技术与精力,大部分项目都是 java 实现的. 这对于非 java 开发者而言很不友好,对于不会编程的用户更加不友好. 为了让更多的人可以使用到这 ...