Coursera在线学习---第一节.梯度下降法与正规方程法求解模型参数比较

一、梯度下降法

优点：即使特征变量的维度n很大，该方法依然很有效

缺点：1）需要选择学习速率α

2）需要多次迭代

二、正规方程法（Normal Equation）

该方法可以一次性求解参数Θ

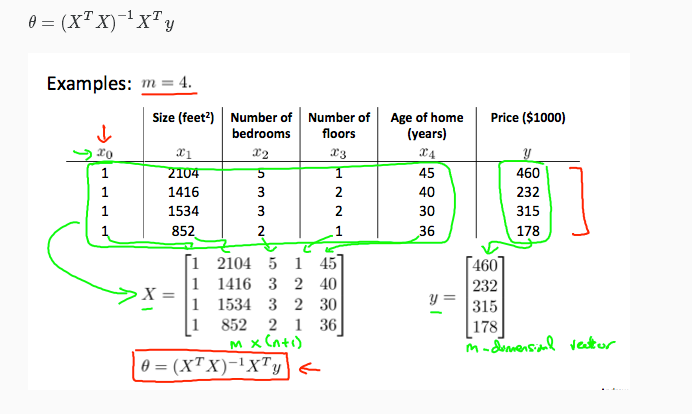
优点：1）不需要选择α

2）不用多次迭代，一次求解

3）正规方程法不需要归一化处理

缺点：逆矩阵的计算量比较大，尤其当特征变量的维度n很大时；计算逆矩阵的运算量大概是矩阵维度的3次方。

总结：当特征变量维度n较大时（n>=10000），选择梯度下降法；当n值较小时(n<10000)，选择正规方程法求解Θ。

备注：求解模型代价函数J(Θ)的最小值方法，本文分析主要针对线性回归模型。对于线性回归模型而言，在特征变量维度不是很大的情况下(n<10000),使用正规方程求解Θ是一个很快捷的方法；但是对于分类问题，  比如逻辑回归这种更加复杂的模型，根本就不能使用正规方程法，而只能使用梯度下降法求救Θ。所以，梯度下降法用的更广泛一些。